18.23 Графика. Окружность

Обозначим черех значение каждой из частей уравнения. Тогда оно эквивалентно системе

Первая подсистема задает часть окружности с центром и радиусом 1, лежащую не ниже прямой . Фактически это верхняя полуокружность такой окружности, т.к. горизонтальная прямая всегда проходит через ее центр. Центры всех таких полуокружностей лежат на горизонтальной прямой .

Вторая подсистема задает часть окружности с центром и радиусом 1, лежащую не ниже прямой . Фактически это верхняя полуокружность такой окружности, т.к. горизонтальная прямая всегда проходит через ее центр. Центры всех таких полуокружностей лежат на вертикальной прямой .

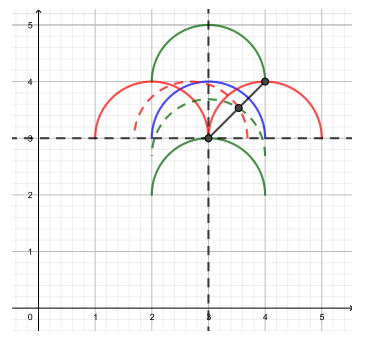
Синее положение достигается при , полуокружности совпадают. Увеличение на положительное число соответствует сдвигу одной полуокружности на вверх, а другой вправо. При уменьшении аналогично вниз и влево.

Крайние положения, в которых еще есть точка пересечения, достигаются при сдвиге на и относительно , то есть при и .

При зеленая полуокружность будет целиком лежать выше прямой , а значит, гарантированно не будет иметь точек пересечения с красной полуокружностью.

При зеленая полуокружность будет целиком лежать ниже прямой , а значит, гарантированно не будет иметь точек пересечения с красной полуокружностью.

В любом положении между крайними, кроме синего, будет одна точка пересечения. Действительно, все такие точки пересечения будут лежать на отрезке между точками и . Получаем .