18.22 Графика. Окружность

По теореме Виета, если рассматривать первое уравнение как квадратное относительно , получаем

Равенство задает верхнюю полуокружность от окружности (которая, заметим, целиком лежит в правой полуплоскости), тогда равенство задает две верхние полуокружности и . Таким образом, система равносильна:

Изобразим график совокупности в области, задающейся неравенством и определим те положения прямой , при которых она с этим графиком (голубой) имеет нечетное число точек пересечения.

:

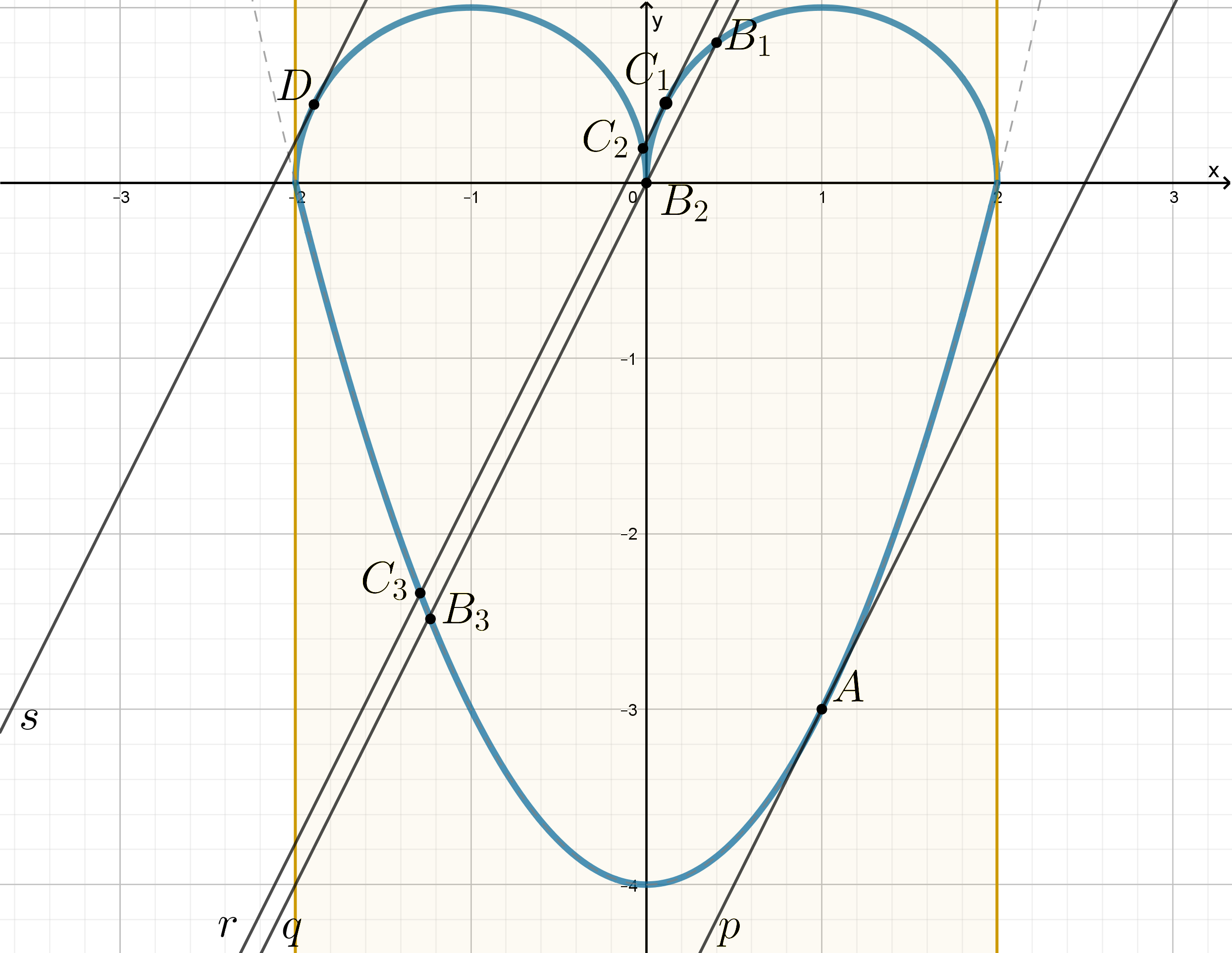
прямая касается параболы в точке ;

:

прямая проходит через “стык” двух полуокружностей — через начало координат (также пересекает правую полуокружность в точке и параболу в точке );

:

прямая касается правой полуокружности в точке (также пересекает левую полуокружность в точке и параболу в точке );

:

прямая касается левой полуокружности в точке

Найдем значения параметра, соответствующие этим положениям прямой.

:

Ищем касание прямой и параболы (через равенство функций и производных в точке касания):

:

прямая проходит через , если

:

прямая касается окружности, если расстояние от центра окружности до прямой равно радиусу окружности:

Нашему положению соответствует большее (так как меньшее соответствует более низкому положению прямой, когда она касается отсутствующей нижней правой полуокружности). Следовательно,

:

аналогично предыдущему пункту

Нашему положению соответствует большее (так как меньшее соответствует более низкому положению прямой, когда она касается отсутствующей нижней левой полуокружности). Следовательно,