18.23 Графика. Окружность

Будем решать задачу графически. Графиком уравнения является уголок, получаемый из уголка (вершина которого находится в точке ) сдвигом на единиц вправо и на единиц вниз. Следовательно, вершина уголка — это точка с координатами и Тогда зависимость между этими координатами следующая: причем заметим, что Следовательно, правая ветвь параболы (то есть часть параболы при ) — траектория, по которой движется вершина уголка

Графиком неравенства является круг (то есть окружность с внутренностью) с центром в точке радиуса

Система имеет единственное решение, когда уголок и круг имеют ровно одну общую точку, то есть одна из ветвей уголка касается окружности а вторая не имеет с окружностью общих точек.

Изобразим графики.

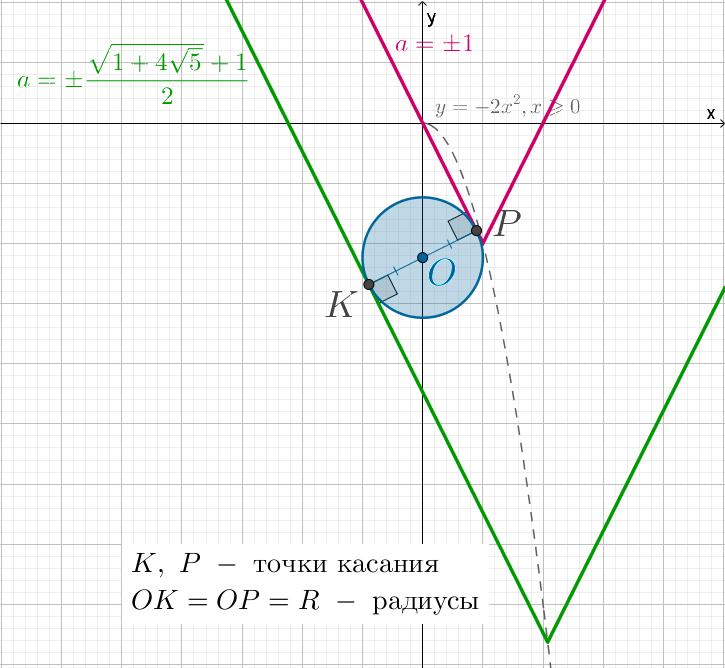
Заметим, что только левая ветвь (назовем ее лучом ) уголка может касаться окружности. Ветвь задается уравнением или же Запишем условие касания луча и окружности через формулу расстояния от точки до прямой: если прямая задана уравнением то расстояние от точки до нее вычисляется по формуле

Заметим, что при использовании этого способа найденные требуют проверки, так как это условие задает касание прямой и окружности, а не луча и окружности.

В случае касания левой ветви и окружности расстояние от центра окружности до должно быть равно радиусу окружности:

Заметим, что не подходит, так как в этом случае точка касания находится не на луче (задаваемом уравнением ), а на его продолжении за вершину уголка, то есть на луче при а эти точки не принадлежат уголку что видно из рисунка:

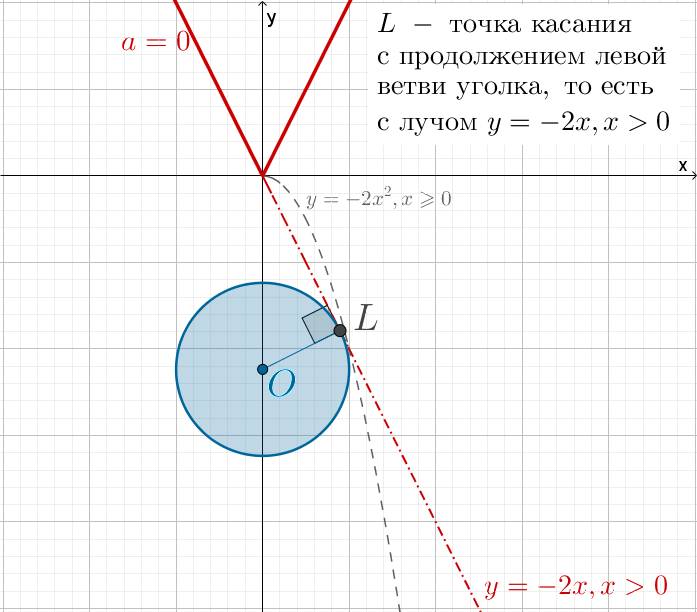
Следовательно, ответ: