3.16 Отношение площадей поверхностей и отношение объемов тел
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде с высотой через точку на боковом ребре, лежащую на расстоянии
от плоскости
основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите
объем полученной меньшей пирамиды, если объем исходной пирамиды равен 54.
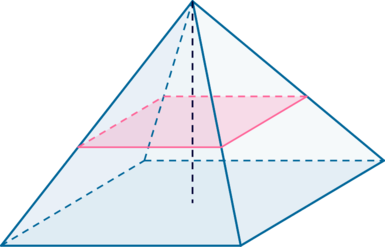
Пусть плоскость провели через точку на ребре
. Так как плоскость параллельна плоскости основания, то она пересечет
боковые грани по прямым
, параллельным соответственно
, причем
– тоже
правильная четырехугольная пирамида.
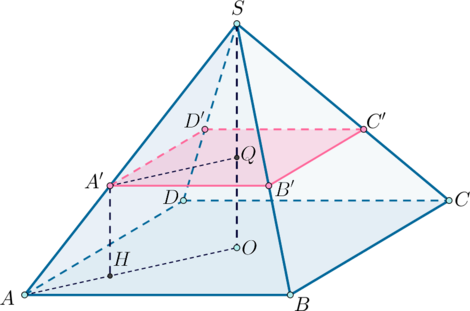
Рассмотрим плоскость . Проведем
(
— высота исходной пирамиды). Тогда
. Следовательно,
это и есть расстояние, равное
, на котором от плоскости основания проведена (розовая) плоскость.
, следовательно,
Также отсюда следует, что .
, следовательно,
Таким образом, объемы маленькой и большой пирамид относятся как
Следовательно, объем маленькой пирамиды равен
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




