18.24 Графика. Функции с модулем: корыто и другие
Ошибка.
Попробуйте повторить позже
Исследуйте траекторию движения графиков функций, записанных в системе
и определите, при каких система имеет бесконечное множество решений.
Обозначим ,
.
- 1)
- Ищем траектории движения графиков.
График
представляет собой “корыто с кривым дном”, а при равенстве нулей подмодульных выражений (при
) уголок. Боковые ветви корыта имеют вид
,
.
Чтобы найти траекторию движения этого графика, можно следить за любой его точкой, например, за точкой
. Следовательно, корыто движется по кривой
.
График
представляет собой уголок, ветви которого имеют вид
,
.
Чтобы найти траекторию движения уголка, можно следить за его вершиной
. Значит, уголок движется по прямой
- 2)
- Определяем, при каком
число решений системы бесконечно.
Заметим, что левая ветвь корыта с левая ветвь уголка параллельны, так как имеют одинаковый коэффициент перед
. То же можно скапзать про их правые ветви. Бесконечное множество решений у системы будет, если корыто и уголок будут иметь бесконечно много точек пересечения, что происходит только в тех случаях, когда одна из боковых ветвей одного графика накладывается на боковую ветвь другого. Это значит, что уравнения, задающие прямые, на которых расположены эти ветви, одинаковы.
Следовательно,
Схематично это выглядит так:
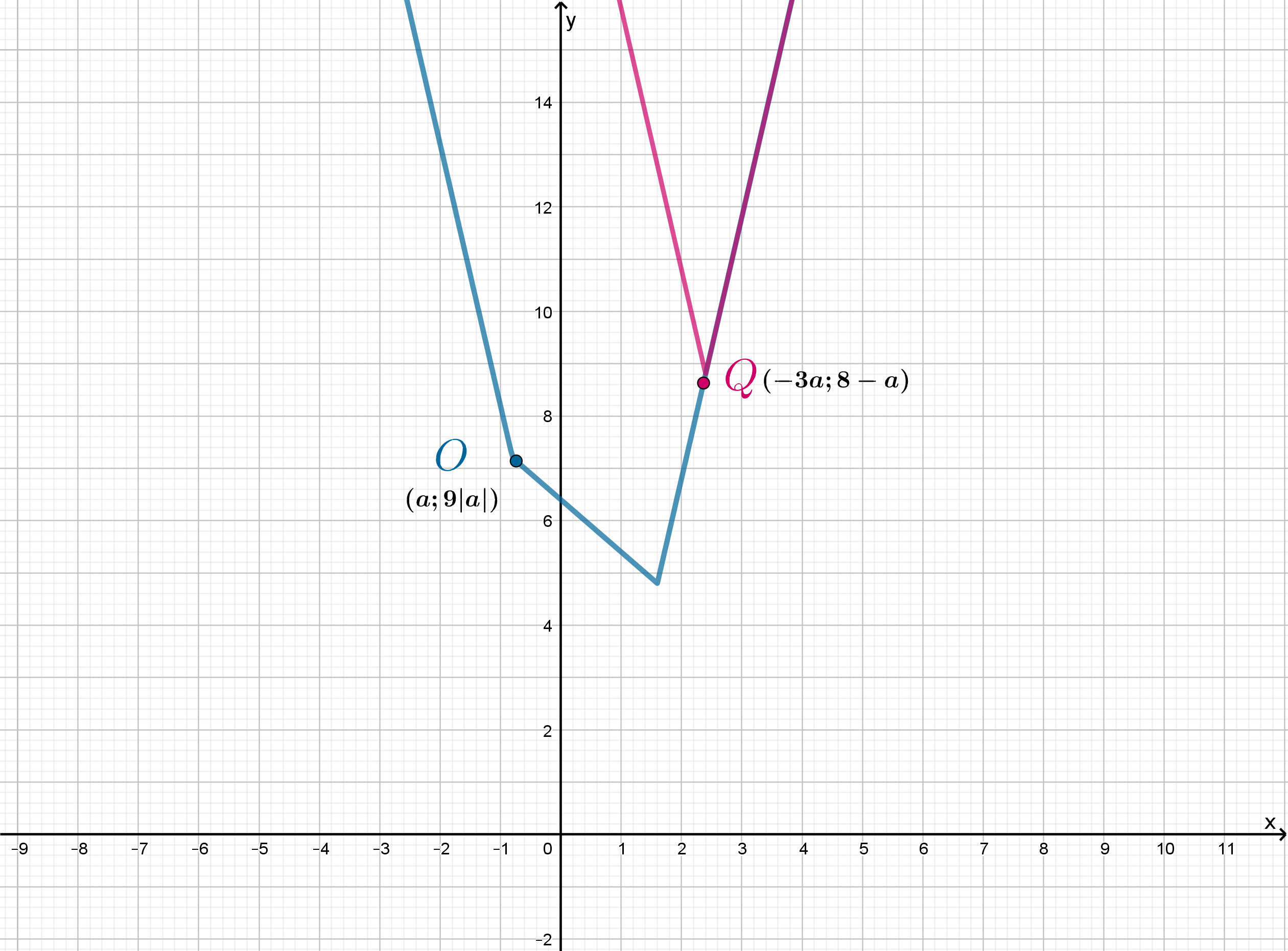
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




