19.03 Задачи формата ЕГЭ

а) Рассмотрим уравнение и найдем его дискриминант:

Так как образуют арифметическую прогрессию, то можно сказать, что где – разность арифметической прогрессии. Тогда

Если уравнение имеет один корень, то

Следовательно, ответ: может. Например, если взять

б) Из пункта а) следует, что

1) Тогда уравнение выглядит так:

Следовательно, первый трехчлен имеет вид

2) Тогда уравнение выглядит так:

Следовательно, второй трехчлен имеет вид

Таким образом, всего существует два приведенных трехчлена, удовлетворяющих заданным условиям.

В обоих случаях мы имеем право делить на так как по условию прогрессия непостоянная, следовательно, разность не равна нулю.

 

в) Пусть имеет два корня, то есть

Пусть – корни. Тогда

Рассмотрим функцию

Ее производная

Следовательно, знаки производной:

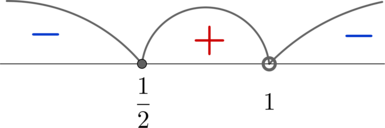
Следовательно, при функция убывает, при функция возрастает.

Из условия следует:

Заметим, что при выполняется условие, что дискриминант положителен:

Таким образом, нужно найти наименьшее значение при Так как при функция убывает, то наименьшее значение будет в точке