19.03 Задачи формата ЕГЭ
Ошибка.
Попробуйте повторить позже
На окружности некоторым способом расставили натуральные числа от 1 до 21. При этом каждое число поставлено по одному разу. Затем для каждой пары соседних чисел нашли разность большего и меньшего.
а) Могли ли все полученные разности быть не меньше 11?
б) Могли ли все полученные разности быть не меньше 10?
в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и
меньшего. Для какого наибольшего целого числа можно так расставить числа, чтобы все разности были не меньше
а) Найдем среди всех чисел число 11. Несложно проверить, что каждое из выражений ниже меньше 11:
Аналогично все выражения ниже также меньше 11:
Тогда какое бы число ни стояло слева или справа от 11, модуль разности между
и 11 меньше 11. Следовательно,
подходящего примера не существует.
б) Приведем пример:

Объясним, как мы его построили. Мы уже поняли, что 11 — особенное число и что рядом с ним могут стоять только числа 1 или 21, чтобы разность между наибольшим из них и 11 была равна 10.
Разобьем все числа на группы:
– числа от 1 до 10;
– числа от 12 до 21.
Заметим, что числа из одной группы не могут стоять рядом, так как разность наибольшего и наименьшего будет меньше 10. Поэтому при расстановке будем чередовать числа из разных групп. Начнем:
Закономерность легко прослеживается. Такими наводящими рассуждениями можно построить искомый пример.
в) Разобьем все числа на три группы:
– группа 1: от 1 до 7;
– группа 2: от 8 до 14;
– группа 3: от 15 до 21.
Все расставленные по кругу числа разобьем на 7 блоков по 3 числа в каждом:
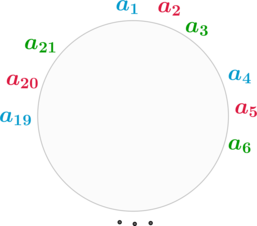
Докажем, что от противного. Пусть
Тогда числа из одной группы не могут находиться в одном блоке. Это так,
поскольку иначе разность либо соседних, либо стоящих через одно чисел по модулю будет меньше 7, так как разность наибольшего и
наименьшего чисел в одном блоке меньше 7
Заметим, что не может быть блока, в котором не будет числа из группы 1: в противном случае 7 чисел из группы 1 должны
разместиться не более чем в 6 блоках. Но тогда по принципу Дирихле найдется блок, в котором будут два числа из группы 1, что
противоречит доказанному условию
Аналогично можно сказать про числа из группы 2 и группы 3.
Поэтому, не умаляя общности, можно считать, что справа от числа из группы 1 стоит число из группы 2, справа от числа из группы 2 — число из группы 3, справа от числа из группы 3 — число из группы 1 и так далее (см. рисунок выше).
Следовательно, в каждом блоке будет ровно один представитель из каждой группы.
Пусть синие числа — представители группы 1, красные — группы 2, зеленые — группы 3.
Найдем число 8 на окружности. Тогда справа или слева рядом с ним и через один от него обязательно будут стоять числа и
из группы 1. Так как наименьшие числа из группы 1 — это 1 и 2, то наибольшая разность среди
и
равна
Получили противоречие, следовательно, предположение неверно. Покажем пример для

а) Нет, не могли
б) Да, могли
в) 6
| Содержание критерия | Балл |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — обоснованное решение в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




