.06 Нелинейные элементы. Диоды (Отсутствует в данном номере в ЕГЭ 2026)
Ошибка.
Попробуйте повторить позже
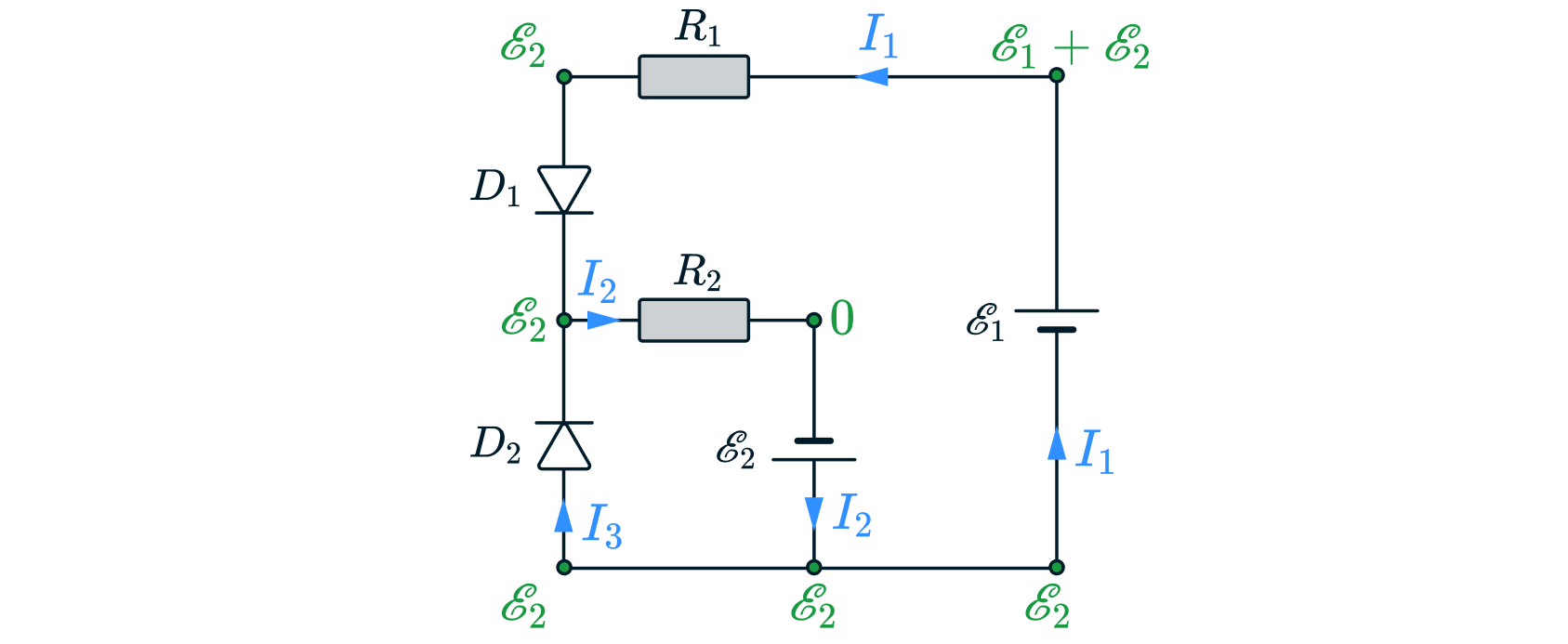
Определите силы токов, протекающих через диоды и
в электрической цепи, параметры которой указаны на рисунке.
Диоды считать идеальными.
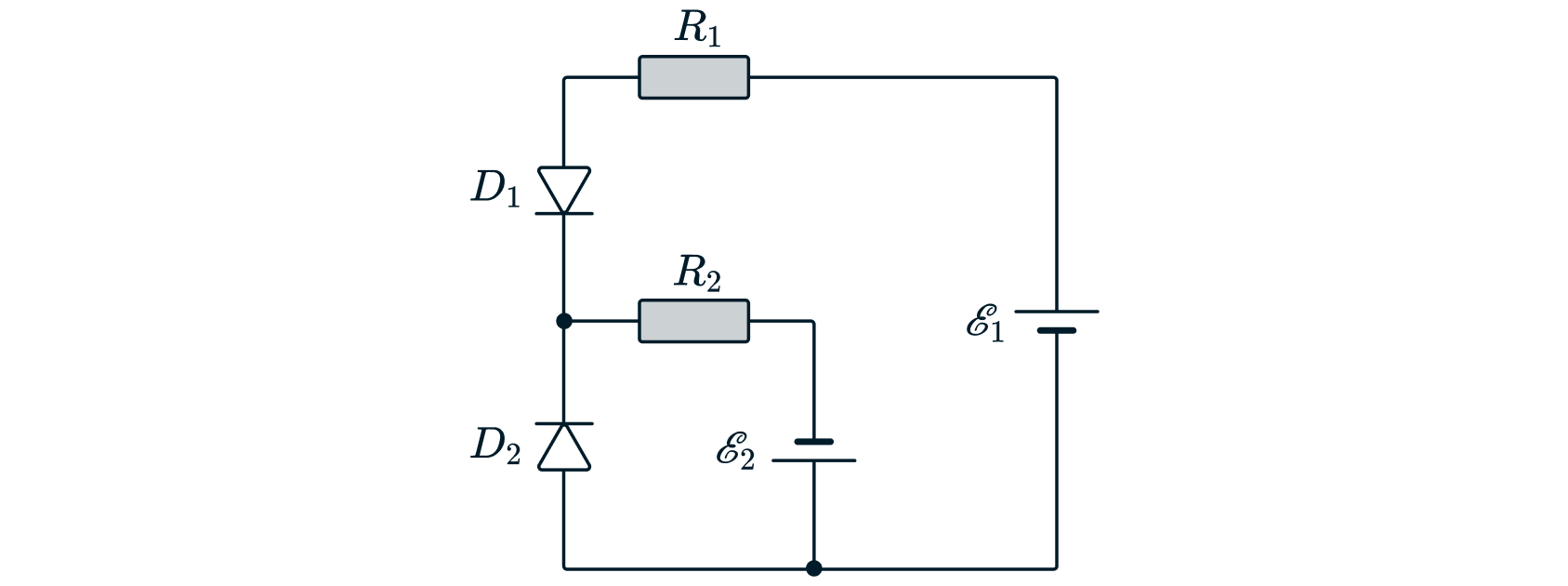
Всего в задаче возможны 4 ситуации:
1. и
закрыты.
2. закрыт,
открыт.
3. открыт,
закрыт.
4. и
открыты.
Рассмотрим каждкую из них, используя метод узловых потенциалов:
1:
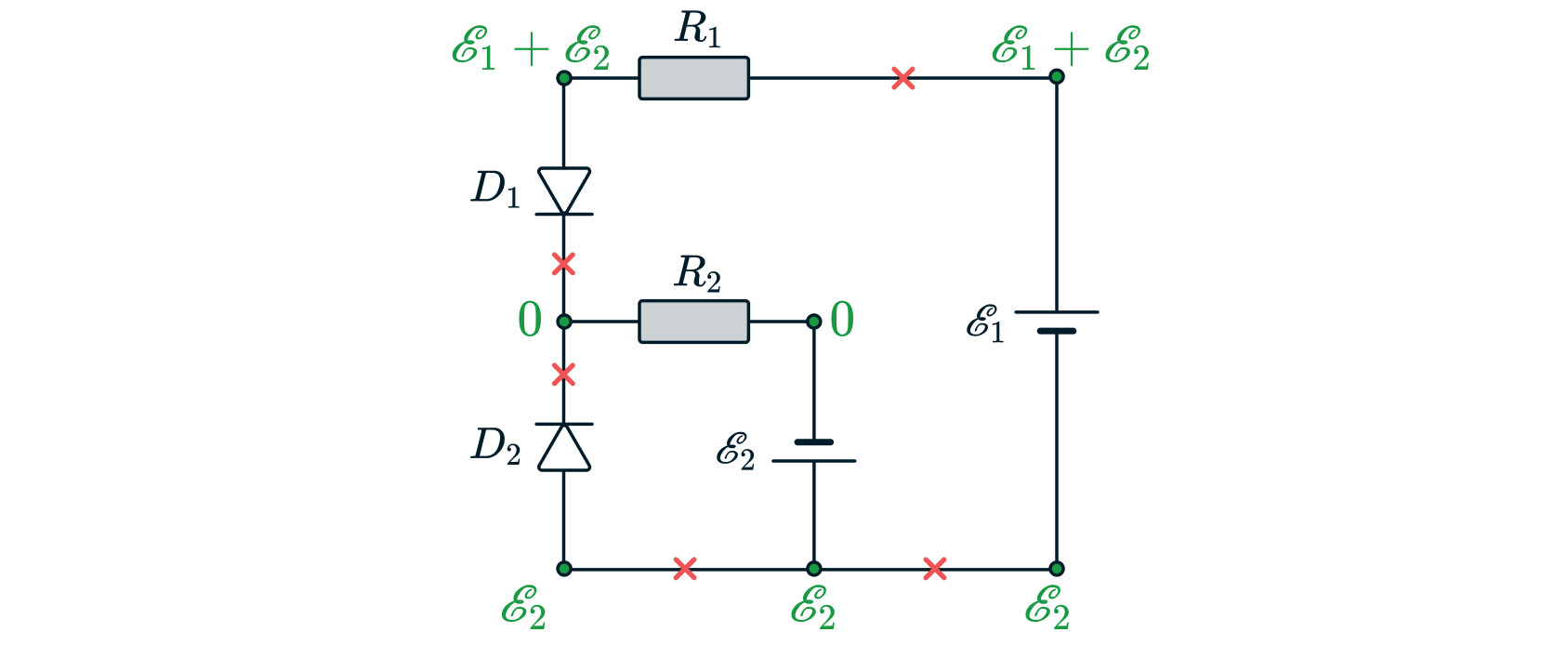
В этом случае тока в цепи нет нигде => потенциал на и на
Не меняется и получается, что оба диода должны быть
открытыми - противоречие, этот вариант нам не подходит.
2:
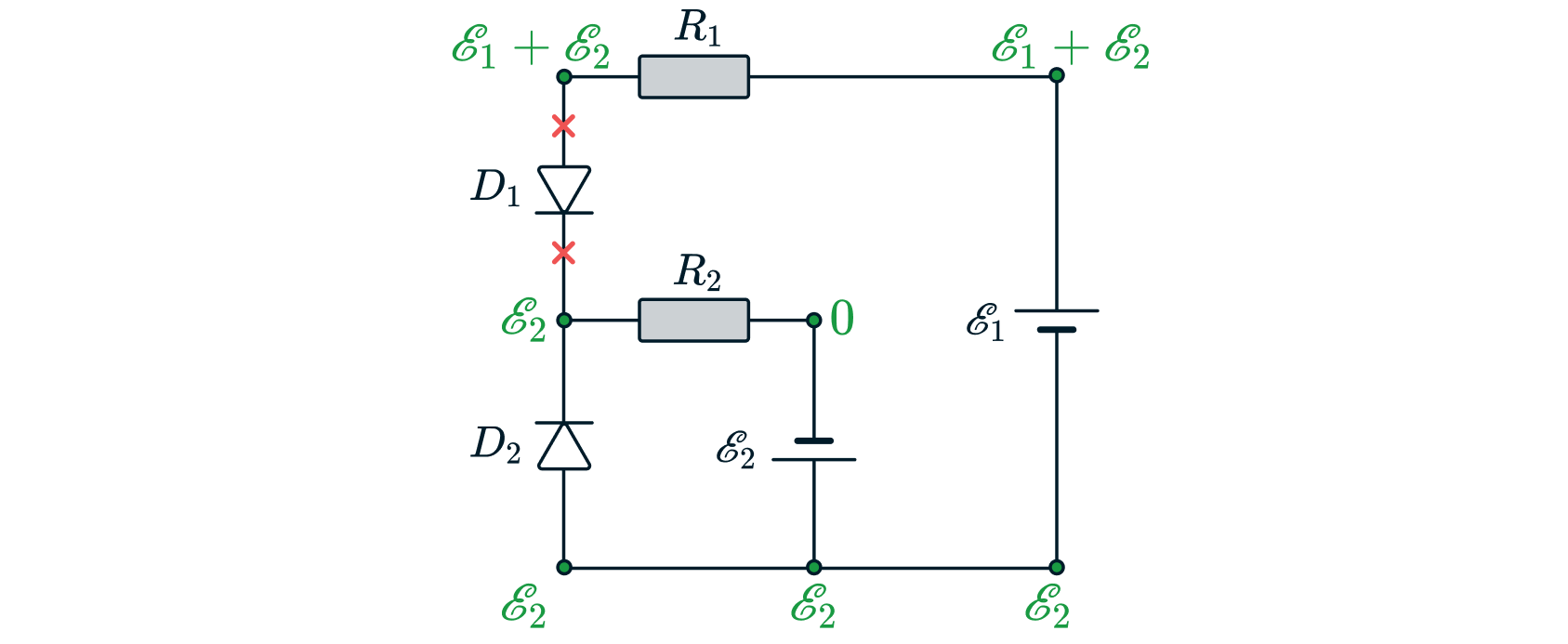
В этом случае тока в цепи нет на => потенциал на нем не меняется. Потенциал между
и
равен
но он меньше
чем
но
закрыт и потенциал между диодами должен быть больше потенциала перед
- противоречие, этот вариант
нам не подходит.
3:
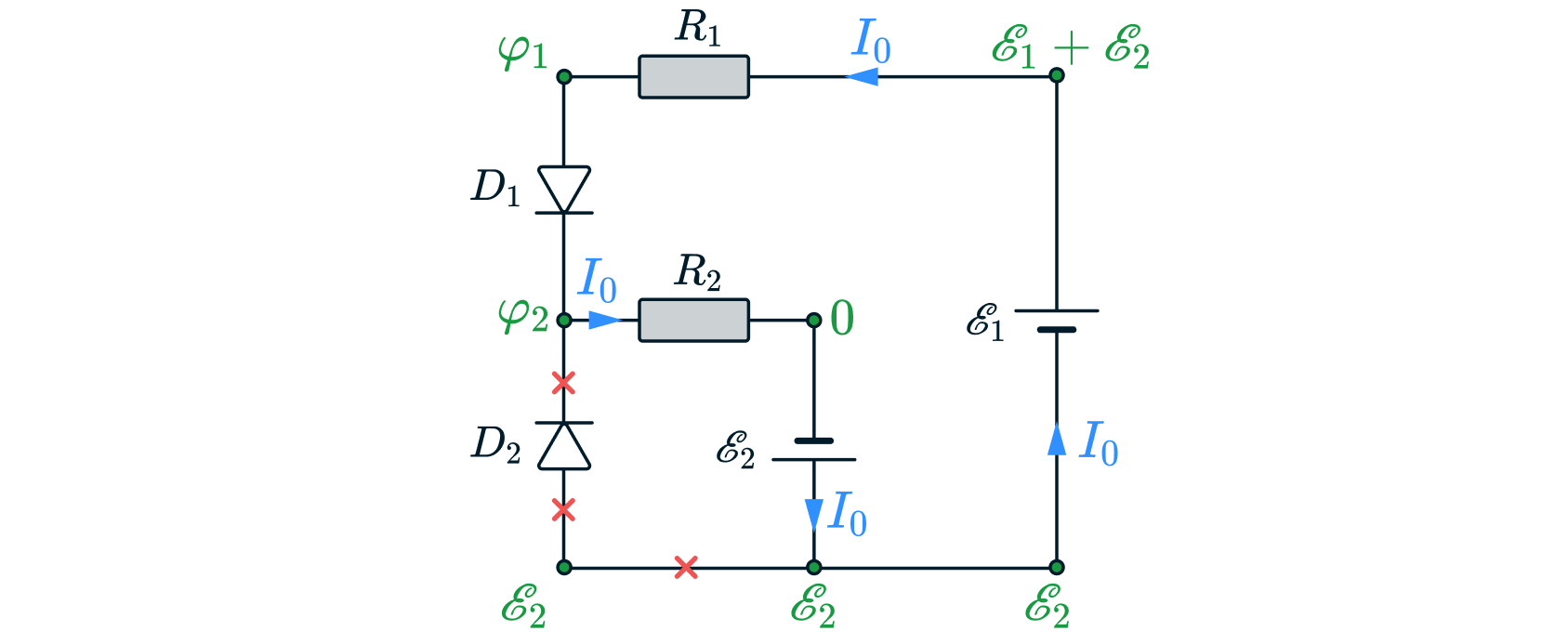
Пусть В этом случае потенциал перед равен
а потенциал между
и
равен
в данном случае для закрытия
требуется
Распишем общий ток:
Для
для (1) из (2) и (3):
4:
В этом случае в цепи будут токи
и
для выполнения необходимых условий должно : решая систему:
1. и
закрыты -нет решений.
2. закрыт,
открыт -нет решений.
3. открыт,
закрыт - если
то
,
4. и
открыты - если
то
,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




