18.27 Метод xOa (параметр как вторая неизвестная)
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых неравенство
имеет хотя бы одно решение.
Упростим первую систему:
Упростим вторую систему:
Заметим, что при
Таким образом, мы получили, что вторая система не имеет решений ни при каких
Далее будем работать только с упрощенной версией первой системы, так как только она дает какие-то решения:
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений системы.
Если некоторая точка плоскости с координатами
принадлежит этому множеству
то для исходной
задачи это означает, что если параметр
принимает значение
то
будет одним из решений системы.
Нас просят найти все такие значения
параметра
при каждом из которых хотя бы одна из точек вида
где
принадлежит множеству решений
изображенному на плоскости
Фактически это
равносильно тому, что горизонтальная прямая
имеет хотя бы одну точку пересечения с множеством
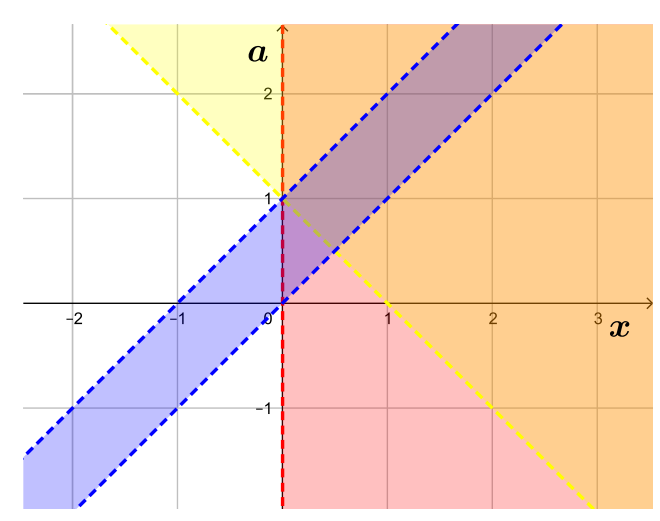
Построим на плоскости множества решений каждого из неравенств системы, а затем пересечем их.
- Множеством решений первого неравенства является полуплоскость «выше» прямой
(выделено желтым).
- Множеством решений второго неравенства является полуплоскость «правее» вертикальной оси
(выделено красным).
- Третье условие задает «полосу» между прямыми
и
(выделено синим):
Пересекая описанные области, получим итоговое множество решений (закрашено зеленым):
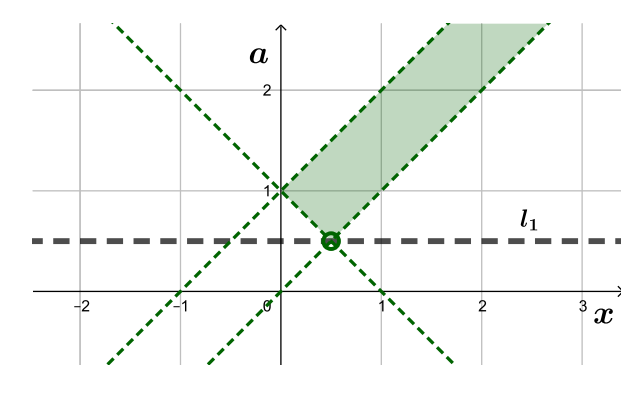
Любая горизонтальная прямая строго выше прямой имеет пересечения с множеством
следовательно, при таких
система имеет решения.
При всех остальных положениях горизонтальной прямой ее пересечение с пусто. Следовательно, исходное неравенство
имеет хотя бы одно решение при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получено
множество значений | 3 |
| С помощью верного рассуждения
получено граничное значение | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




