18.27 Метод xOa (параметр как вторая неизвестная)
Ошибка.
Попробуйте повторить позже
Найдите все значения при которых уравнение
имеет ровно два решения.
Способ 1 (алгебраический)
Данное уравнение равносильно
Заметим, что если оба дискриминанта уравнений и
отрицательны, то
совокупность не будет иметь решений. Рассмотрим следующие случаи, где
и
— дискриминанты уравнений
и
соответственно.
1) следовательно,
Тогда уравнение (1) имеет единственный корень который подходит под
условие
При
дискриминант
следовательно, уравнение (2)
имеет два корня
Заметим, что оба этих корня подходят под условие
Следовательно, вся совокупность имеет три решения. Этот случай нам не
подходит.
2) следовательно,
Тогда уравнение (2) имеет единственный корень который подходит под
условие
При
дискриминант
следовательно, уравнение (1)
имеет два корня
и
причем оба подходят под условие
Но,
учитывая, что один из корней уравнения (1) совпал с корнем уравнения (2),
совокупность будет иметь два решения:
и
Следовательно, этот
случай нам подходит.
Мы рассмотрели случаи, когда один из дискриминантов равен нулю, теперь рассмотрим оставшиеся случаи, которые нам могут подойти.
3) и
Тогда
Следовательно, уравнение (1) имеет два корня уравнение (2)
не имеет корней. Для того, чтобы совокупность имела два решения, нужно, чтобы
оба получившиеся корня удовлетворяли условию
Для этого достаточно,
чтобы меньший корень удовлетворял этому условию:
Учитывая, что мы рассматриваем случай, когда получаем итоговые
подходящие значения для
4) и
Тогда
Следовательно, уравнение (1) не имеет корней, а уравнение (2) имеет два корня
Для того, чтобы совокупность имела два решения, эти корни
должны удовлетворять условию
Для этого достаточно, чтобы больший
корень удовлетворял этому условию:
Учитывая, что в нашем случае получаем подходящие значения для
5) и
Тогда
Следовательно, оба уравнения имеют по два корня.
Пусть
Заметим, что корни и
симметричны относительно 3, а корни
и
— относительно 1, то есть
находится правее 3,
— левее 1. При
значениях
корни
и
всегда будут удовлетворять условиям
и
соответственно. Следовательно, чтобы совокупность имела
два решения, корни
и
НЕ должны удовлетворять этим условиям
соответственно:
Учитывая, что в нашем случае получаем окончательные
подходящие значения для
Тогда исходное уравнение имеет ровно два решения при
Способ 2 (графический).
Будем рассматривать параметр как переменную. Построим в системе
координат
множество
решений системы. Если некоторая точка плоскости
с координатами
принадлежит этому множеству
то для исходной
задачи это означает, что если параметр
принимает значение
то
будет
одним из решений системы. Нас просят найти все такие значения
параметра
при каждом из которых две точки вида
, где
принадлежат
множеству решений
изображенному на плоскости
Фактически это
равносильно тому, что горизонтальная прямая
имеет две точки
пересечения с множеством
Наше уравнение равносильно
Пусть — множество, задающееся полученной совокупностью. Тогда
—
это объединение двух частей парабол (голубой и зеленой), изображенных на
рисунке.
Заметим, что параболы пересекаются в двух точках и
, расположенных
на прямой
:
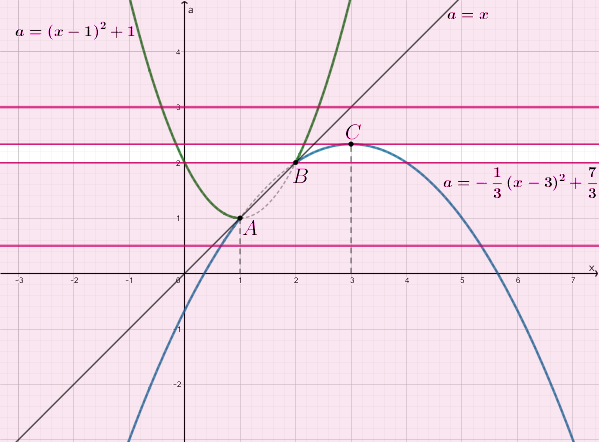
Таким образом, от обеих парабол нужно взять части, соответствующие
или
Также на рисунке розовым цветом обозначена область, в которой может
находиться прямая если требуется две точки пересечения этой прямой с
множеством
Таким образом, нам подходят все прямые, лежащие ниже прямой, проходящей
через и лежащие выше прямой, проходящей через
Точка имеет координаты
Следовательно,
или
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получены
все значения | 3 |
| С помощью верного рассуждения
получены не все значения | 2 |
| Задача верно сведена к исследованию взаимного расположения графика функции и прямой (аналитически или графически) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




