18.27 Метод xOa (параметр как вторая неизвестная)
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых неравенство
не имеет решений.
Рассмотрим функции и
. Тогда неравенство примет вид
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений неравенства. Если
некоторая точка плоскости с координатами
принадлежит этому множеству
то для исходной задачи это означает, что если
параметр
принимает значение
то
будет одним из решений неравенства. Нас просят найти все такие значения
параметра
при каждом из которых не существует точек вида
,
, принадлежащих множеству решений
изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая
не имеет точек пересечения с множеством
.
Построим графики функций и
. Для этого требуется исследовать данные функции.
-
Функция
является композицией двух функций:
и
, то есть
. Функция
возрастающая, следовательно, характер монотонности функци
определится, если исследовать функцию
:
Производная равна нулю при
и не существует при
, следовательно, эти точки разбивают ее область определения на промежутки, знаки на которых следующие:

Учитывая, что
, на промежутке
функция
возрастает, а при
убывает.
Так как
то при
функция
убывает, а при
эта функция возрастает (композиция двух функций одинакового характера монотонности — возрастающая, а разного — убывающая).
- При
имеем
.
- При
имеем
.
- При
имеем
.
Тогда график функции
выглядит следующим образом:

- При
-
Функция
является композицией двух функций:
и
, то есть
. Функция
возрастающая, следовательно, характер монотонности функци
определится, если исследовать функцию
, у которой промежутки возрастания/убывания такие же, как у функции
.
Следовательно, учитывая, что
при
и
,
функция
возрастает, а при
,
функция убывает.
Так как
то при
и
,
функция
возрастает, а при
,
функция убывает (композиция двух функций одинакового характера монотонности — возрастающая, а разного — убывающая).
- При
имеем
.
- При
имеем
.
- При
имеем
.
Тогда график функции
выглядит следующим образом:
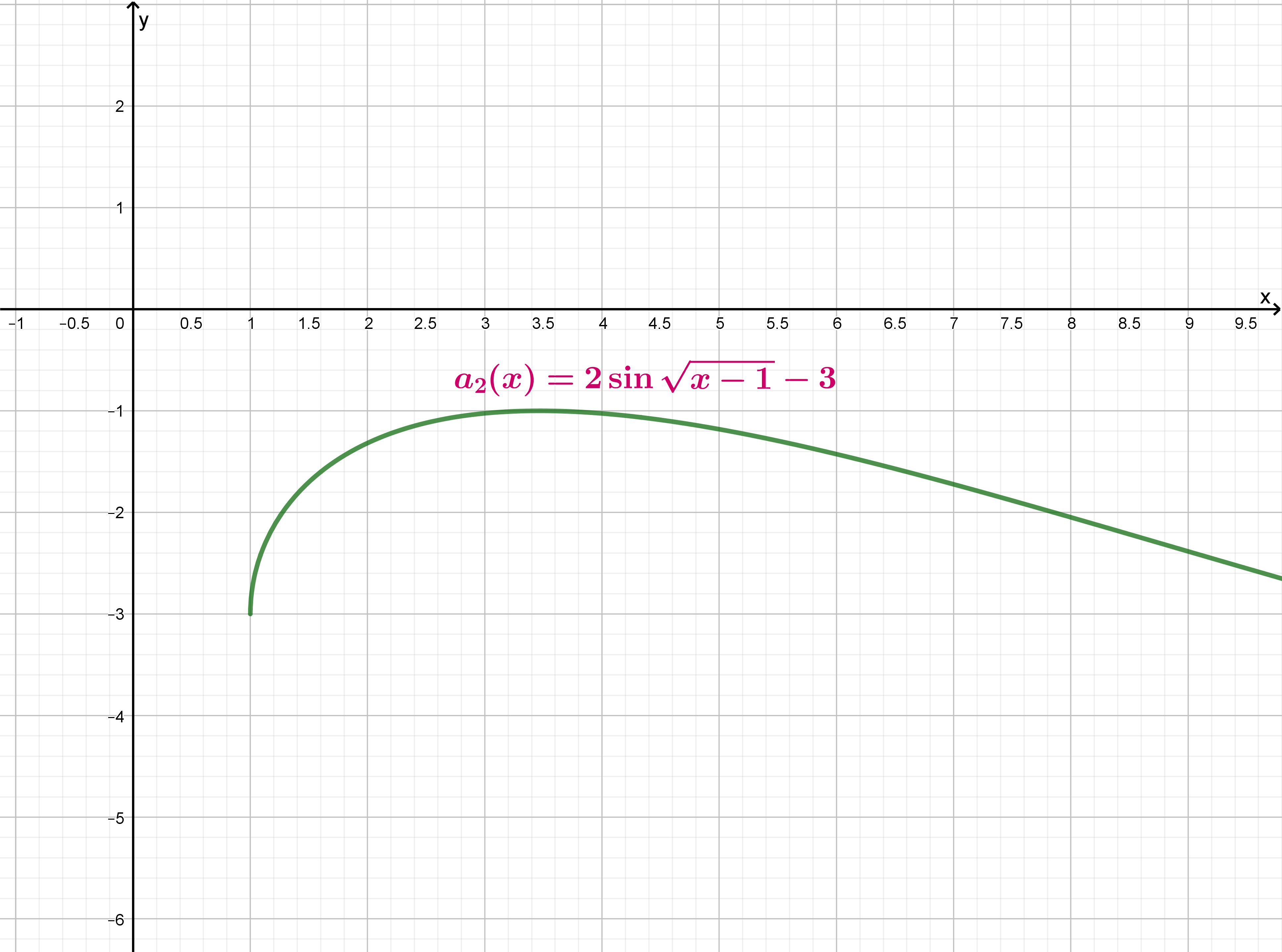
- При
Изобразим оба графика на одной координатной плоскости. Для этого найдем значения функций в некоторых точках:
Тогда решением неравенства будет множество , которое является объединением области 1 и области 2, где
область 1: пересечение областей над графиками функций и
, включая график
и исключая график
;
область 2: пересечение областей под графиками функций и
, включая график
и исключая график
.

Исходное неравенство не имеет решений, если горизонтальная прямая не пересекает закрашенную область
, то есть
находится в полосе между
(включая это значение) и
(исключая это значение). Значит, ответ:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




