14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

Пусть дана пирамида с вершиной .

 — описанная около сферы с центром в точке      — точка пересечения биссекторных плоскостей внутренних двугранных углов при основании пирамиды.

Пусть — точки касания сферы с основанием и боковыми гранями пирамиды (см.рис.). Тогда для . Докажем, что принадлежит биссекторной плоскости произвольного двугранного угла при основании пирамиды.
Докажем лемму. Если точка равноудалена от граней двугранного угла, то она лежит в биссекторной плоскости этого угла.
Пусть плоскости и образуют двугранный угол (назовем его ) с ребром . Проведем , . Проведем . Тогда — наклонная, а , — ее проекции на плоскости и соответственно. Следовательно, по ТТП , , то есть — линейный угол двугранного угла . как прямоугольные по катету и гипотенузе (, — общая). Следовательно, и равны, а также являются линейными углами двугранных улов между гранями угла и плоскости, построенной на прямых и . Следовательно, лежит в биссекторной плоскости угла .

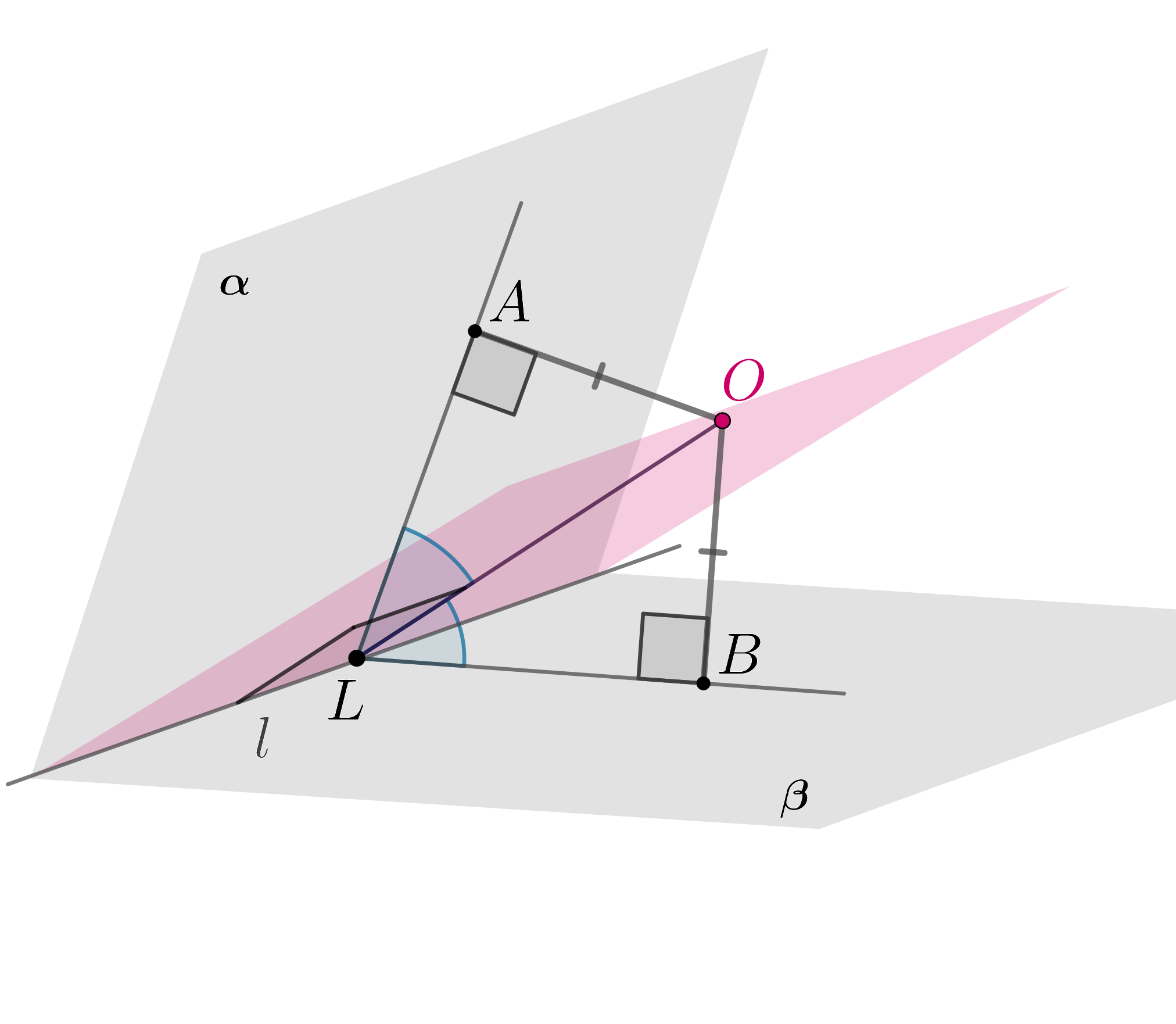
Так как равноудалена от граней двугранных углов (например, так как , следовательно, лежит в биссекторной плоскости двугранного угла между основанием и гранью ), образованных основанием и произвольной боковой гранью, то лежит в биссекторных плоскостях этих двугранных углов.

 — точка пересечения биссекторных плоскостей внутренних двугранных углов при основании пирамиды      — центр сферы, вписанной в  

Докажем, что точка равноудалена от основания и боковых граней пирамиды. Опустим перпендикуляр на плоскость и перпендикуляр на плоскость . Так как лежит в биссекторной плоскости угла между и , то равноудалена от граней этого двугранного угла, следовательно, .

Аналогично мы получим, что , , откуда получим , . Следовательно, точка равноудалена всех граней пирамиды, значит, является центром вписанной в пирамиду сферы.