14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус
Ошибка.
Попробуйте повторить позже
Дана пирамида с основанием
.
а) Докажите, что если основание высоты
пирамиды
лежит
внутри
и все боковые грани пирамиды наклонены к плоскости основания
под одним и тем же углом (то есть двугранные углы при основании пирамиды
равны), то в эту пирамиду можно вписать сферу.
б) Основанием пирамиды служит квадрат
со стороной 15, а
радиус вписанной в пирамиду сферы равен 3. Найдите высоту пирамиды, если она
совпадает с ребром
.
а) Будем сокращенно двугранный угол с ребром называть ”ДУ при
“.
1) основание высоты
лежит внутри
; 2)
двугранные углы при основании равны
в
вписана сфера
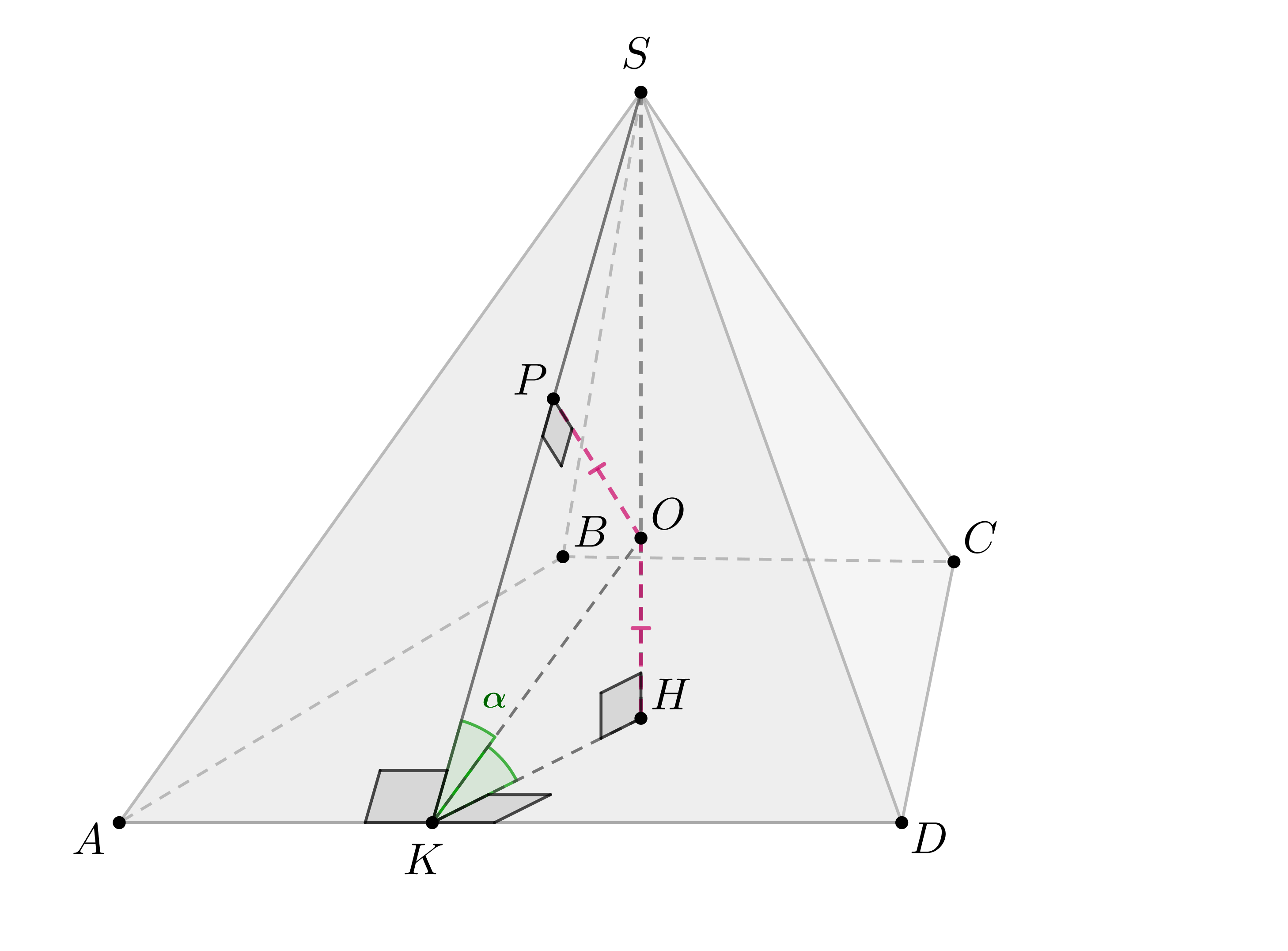
Пусть все ДУ при сторонах основания равны
,
. Проведем
, тогда по ТТП наклонная
. Значит,
— линейный
угол ДУ при
, то есть
. Если
— биссектриса
, то
—- точка пересечения биссекторной плоскости ДУ при
(действительно,
— линейные
углы ДУ, образованных плоскостью
и
или
). Тогда
, где
.
Заметим, что . Рассмотрим
:
Так как длина отрезка не зависит от выбора ДУ при ребре основания, то
— точка пересечения с
всех биссекторных плоскостей ДУ при сторонах
основания пирамиды. Таким образом, расстояния от
до всех граней
пирамиды равны
, следовательно,
— центр вписанной сферы,
—
радиус.
Чтд.
б) Пусть — радиус вписанной сферы,
,
. Так как
,
,
, то по ТТП наклонные
,
. Заметим, что
как прямоугольные по двум катетам,
следовательно,
. Известна формула
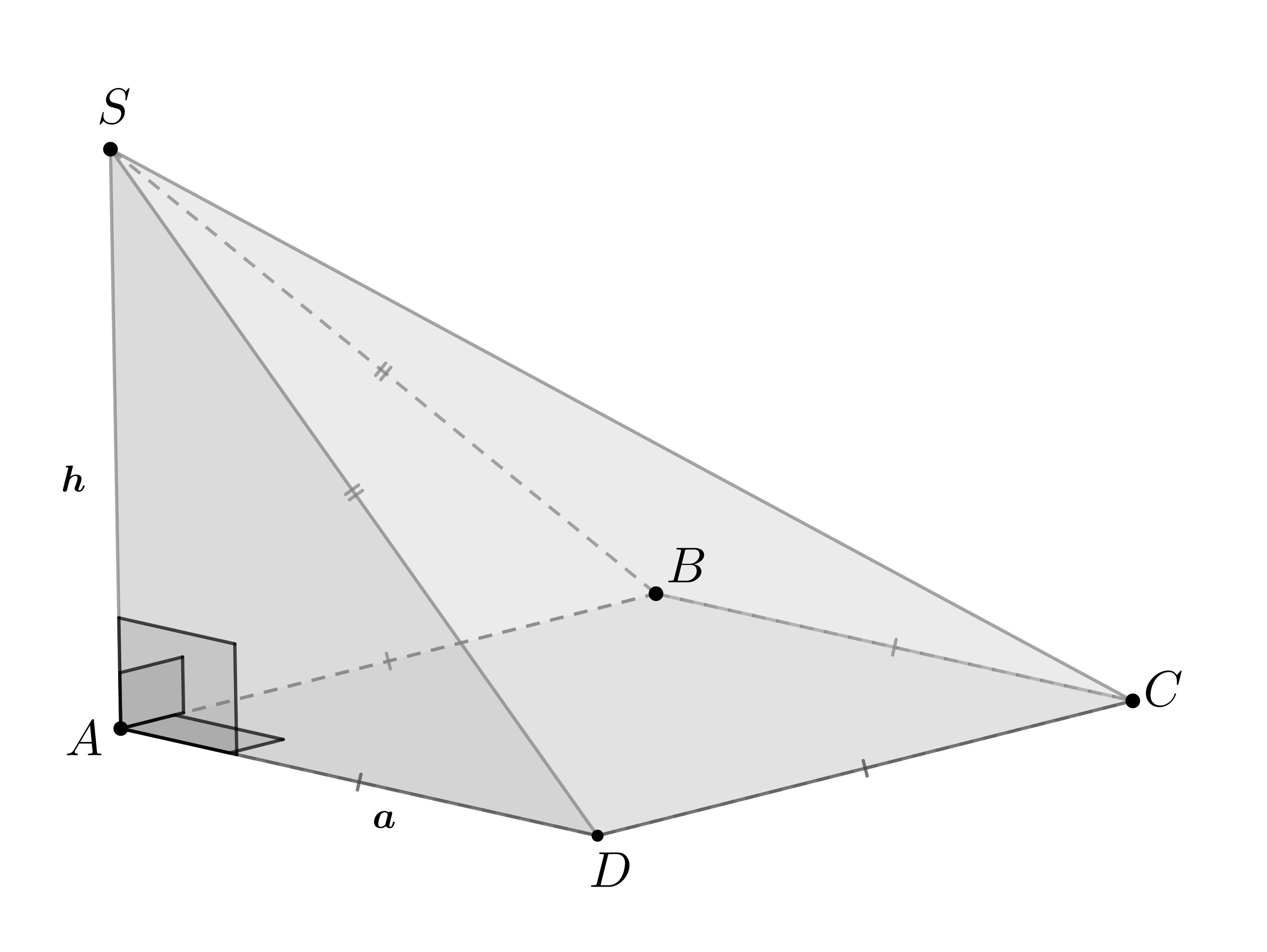
Преобразуем получившееся уравнение и найдем :
Подставим и получим
б)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




