14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

а) Пусть — высота пирамиды, — центр вписанной в пирамиду сферы, —- центр описанной около пирамиды сферы. Так как пирамида правильная, то .

Точки    и    совпадают    Сумма плоских углов при вершине    равна  

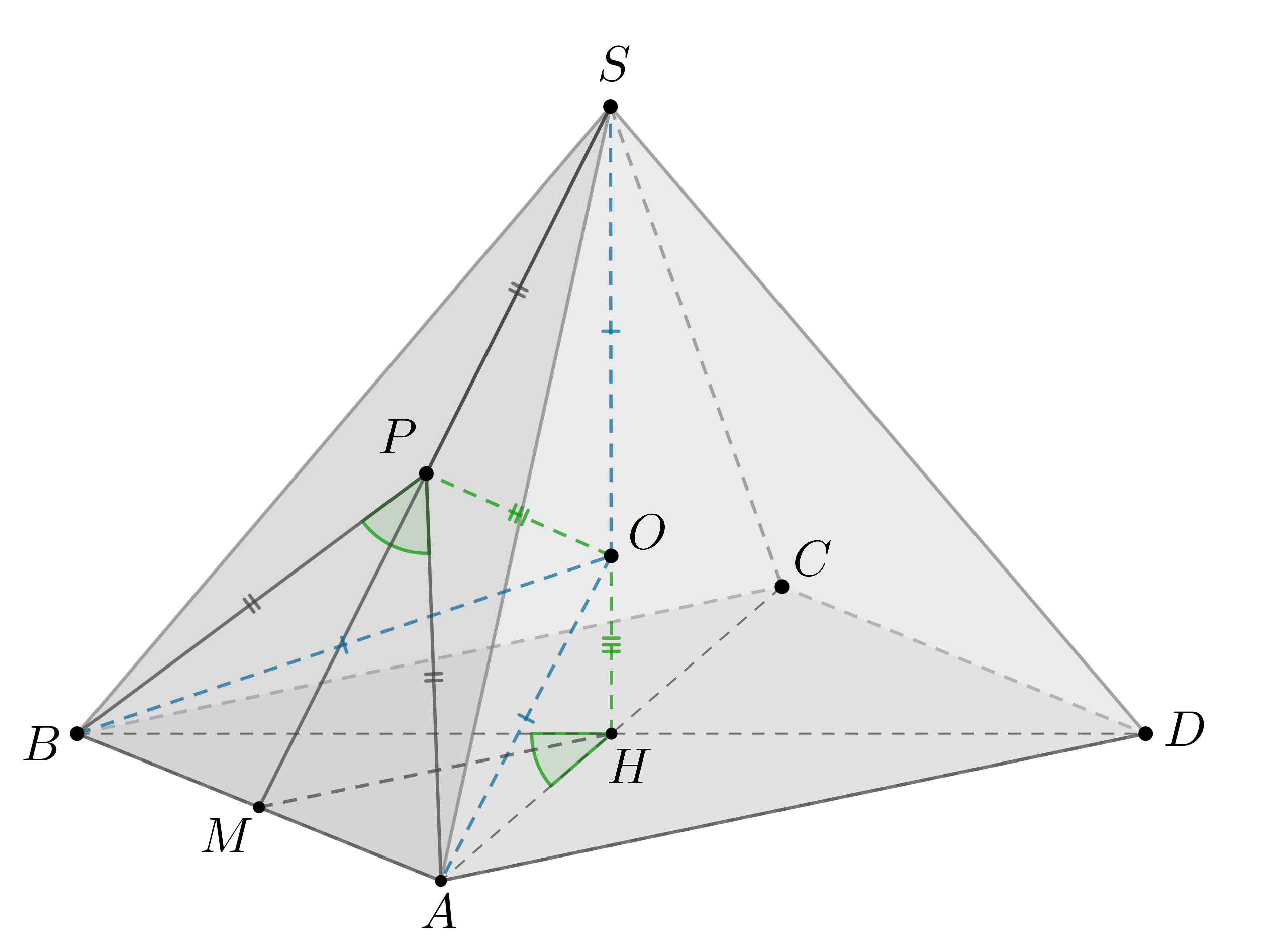
Пусть — центр описанной и вписанной сфер. Тогда — радиус описанной сферы. Проведем , тогда по ТТП . Проведем . Так как — точка касания вписанной сферы и гранью .

Заметим, что — проекции , , на плоскость . Так как наклонные равны, то и проекции равны, следовательно, — центр окружности, описанной около . Тогда (центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу).

Так как равноудалена от сторон , является биссектрисой этого угла и . Тогда как равнобедренные с равными основаниями и высотами, проведенными к этим основаниям.

Значит, . Тогда . Тогда сумма четырех равных углов при вершине равна

Чтд.

Сумма плоских углов при вершине    равна      Точки    и    совпадают

Пусть — центр вписанной в пирамиду сферы. Пусть , , , .

Если сумма плоских углов при вершине равна , то, так как эти углы равны, получаем . Выше доказывалось, что , откуда .

Пусть — центр окружности, описанной около равнобедренного . Тогда и (центральный угол в два раза больше вписанного, опирающегося на ту же дугу). Отсюда следует, что , то есть — проекции на . Так как проекции равны, то равны и наклонные: и — центр описанной около пирамиды сферы.

б) Пусть — центр вписанной в пирамиду сферы, , — радиусы. Так как равноудалена от граней , , , то — линия пересечения биссекторных плоскостей при ребрах и , следовательно, любая точка прямой равноудалена от , , центр второй сферы . Пусть . Так как две сферы касаются друг друга, то (сумма радиусов).

с коэффициентом подобия , следовательно, — средняя линия , значит, .

Пусть , тогда и по теореме Пифагора в : .

Пусть . Из следует, что

Тогда . Пусть — середина и . Тогда — центр описанной около пирамиды сферы. Имеем

. Следовательно,