14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

а) Пусть вершины расположены на диагонали , тогда вершины — на диагонали куба . Действительно, так как тетраэдр правильный, то противоположные ребра тетраэдра перпендикулярны, следовательно, . Диагонали куба, перпендикулярные диагонали грани куба — это или . Без ограничения общности можно выбрать любую из этих двух.

По свойству правильноо тетраэдра если — середина , то . Так как , то , то есть —- точка пересечения диагоналей грани . Так как — середина , то , следовательно, и расположены на симметрично относительно .

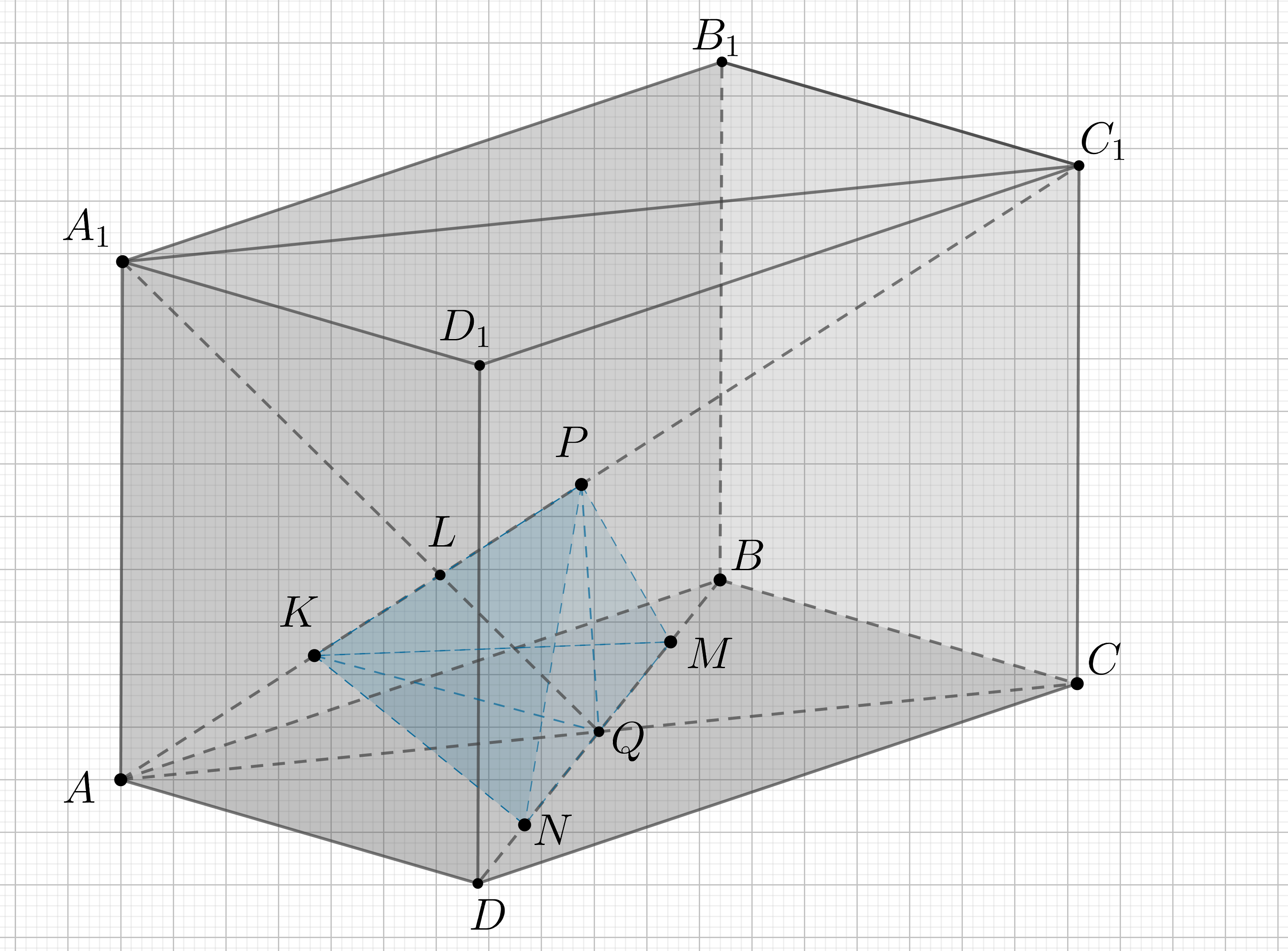
б) Так как все грани правильного тетраэдра равны и являются правильными треугольниками, то и высоты этих граней равны, следовательно, . Тогда медиана в является и высотой. Тогда точки и расположены на симметрично относительно .

Если — ребро тетраэдра, то . Тогда

Теперь рассмотрим . Пусть — ребро куба. . Следовательно, . Так как , то получаем, что .

Пусть пересекает в точке . Тогда . Следовательно, . То есть точка точка совпадает с точкой .

Из с . С другой стороны, . Отсюда следует, что ребро тетраэдра .

Пусть . Тогда — центр описанной сферы — лежит на . Плоскость является биссекторной плоскостью для двугранного угла при ребре , следовательно, .

Рассмотрим теорему Менелая для и прямой :