14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

а) Боковые грани пирамиды имеют одинаковые углы с основанием, значит, основание высоты пирамиды — центр вписанной в основание окружности. Действительно, опустим высоту и проведем перпендикуляры , , к сторонам основания. Тогда по ТТП перпендикулярна той стороне основания, к которой она проведена. Следовательно, — линейные углы двугранных углов при сторонах основания. Они равны, следовательно, по острому углу и общему катету. Следовательно, , следовательно, — центр вписанной в основание окружности.

Так как основания цилиндра параллельны, то верхнее основание — окружность, вписанная в треугольник , являющийся сечением пирамиды плоскостью, параллельной основанию . . Двугранные углы при сторонах основания пирамиды равны двугранным углам при основании пирамиды . Следовательно, — центр вписанной в окружности. Эта окружность и есть верхнее основание цилиндра.

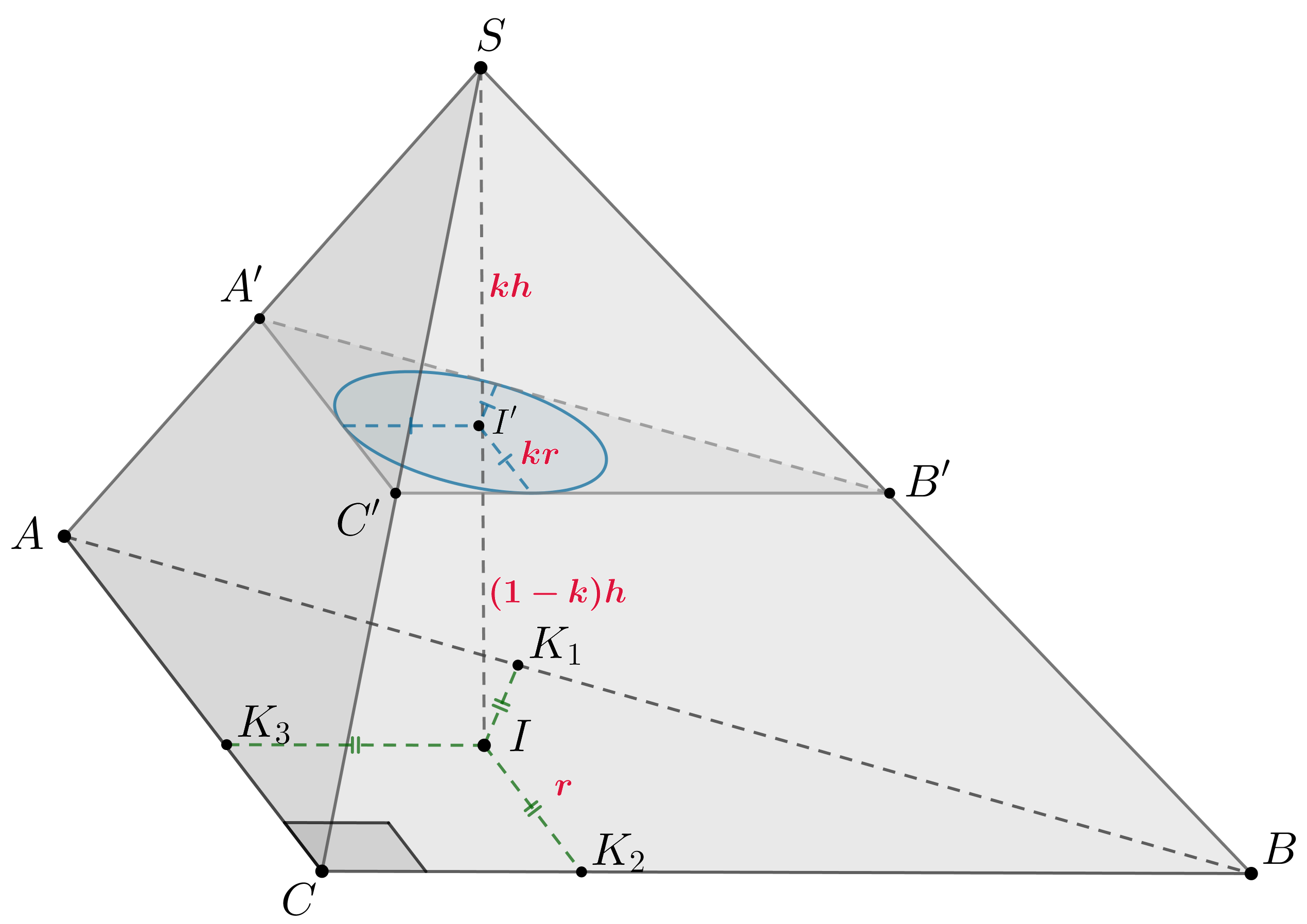
Так как , то , , . Пусть , тогда плоскость сечения делит высоту в отношении , считая от . Тогда по Фалесу все боковые ребра пирамиды делятся в таком же соотношении. Рассмотрим и . Так как , то эти треугольники подобны, следовательно, .

Таким образом мы получаем, что все элементы пирамиды относятся к соответствующим элементам пирамиды с коэффициентом .

Пусть — радиус вписанной в окружности, — высота пирамиды . Тогда — радиус вписанной в окружности, — высота . Тогда .

Следовательно, площадь боковой поверхности цилиндра равна

Рассмотрим выражение .

Тогда

б) Так как условие ”боковые грани наклонены к плоскости основания под одним и тем же углом“ и ”двугранные углы при ребрах основания равны“ – это одно и тоже, то речь о пирамиде, основание высоты которой — центр вписанной окружности. В предыдущем пункте мы вывели формулу для площади боковой поверхности вписанного цилиндра. Для того, чтобы ей воспользоваться, нужно найти радиус вписанной в окружности и высоту пирамиды.

Рассмотрим . Есть формула, связывающая радиус вписанной в прямоугольный треугольник окружности с его катетами и гипотенузой :

Рассмотрим прямоугольный

Заметим, что — квадрат, поому что это прямоугольник с равными смежными сторонами. Следовательно, . Тогжа получаем

Теперь имеем

Следовательно, возможны два варианта для значений радиуса основания цилиндра: он может быть равен числам или