14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

а) Если двугранные углы при основании пирамиды равны, то основание ее высоты — центр вписанной в основание пирамиды окружности. Действительно, проведем перпендикуляры к сторонам ромба. Тогда по ТТП перпендикулярны соответствующим сторонам ромба. Тогда — линейный угол двугранного угла при стороне основания. Тогда , как прямоугольные по острому углу и общему катету . Следовательно, точка равноудалена от сторон , то есть является центром вписанной в окружности.

Чтд.

б) Докажем вспомогательную лемму: если отрезок пересекают две параллельные плоскости и , проходящие через и , и делят его в отношении , то любой другой отрезок , пересекающий плокости в точках и , делится этими плоскостями в том же отношении. А также относится к как .

Проведем перпендикуляр к плоскостям, причем . Тогда как прямоугольные и общим острым углом . Следовательно, .

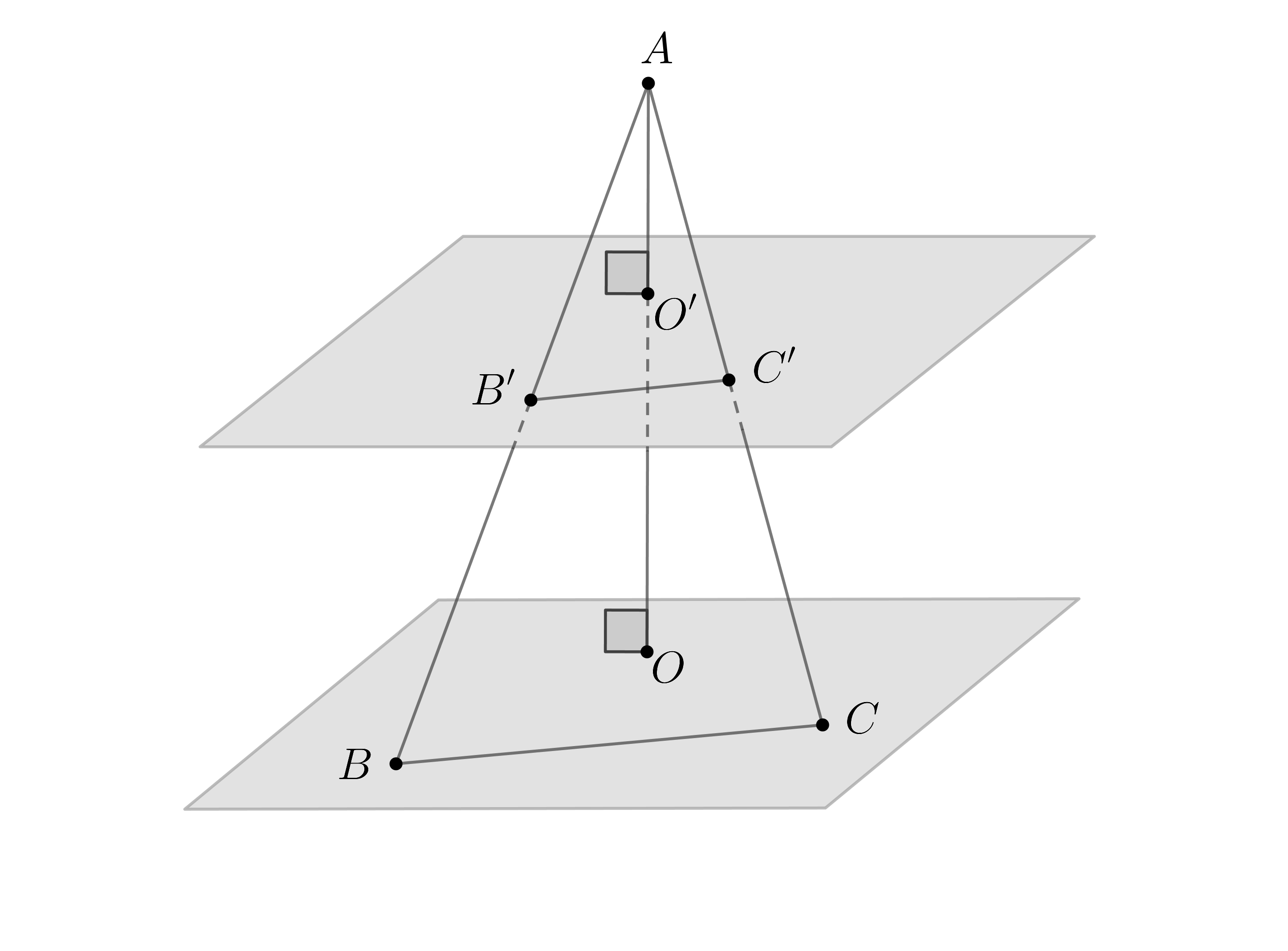
Проведем произвольный отрезок , пересекающий плоскость в точке , . Рассмотрим и . Они подобны как прямоугольные по общему острому углу. Следовательно, , то есть .

Рассмотрим : по двум пропорциональным сторонам и углу между ними, следовательно, .

Пусть — сечение пирамиды плоскостью , — радиус вписанной в этот ромб окружности, — радиус вписанной в окружности. По лемме получаем, что .

Тогда объем цилиндра равен

Рассмотрим Пусть , . Проведем . как прямоугольные по острому углу, следовательно, . Так как , то — равносторонний с высотой . Так как высота правильного треугольника со стороной равна , то . Следовательно,

Следовательно,

Тогда