14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

а) Если сфера описана около параллелепипеда, то ее центр находится на одинаковом расстоянии от всех вершин параллелепипеда.

Будем сокращенно записывать как .

Пусть — центр сферы. Расстояния от точки до вершин одинаковы и равны .

Проведем . Рассмотрим , , , . Они равны как прямоугольные по общему катету и гипотенузе. Следовательно, равноудалена от вершин , то есть — центр описанной около окружности. Если около параллелограмма можно описать окружность, то он — прямоугольник.

Аналогично поступаем с каждой гранью и получаем, что все его грани — прямоугольники. Это по определению и есть прямоугольный параллелепипед.

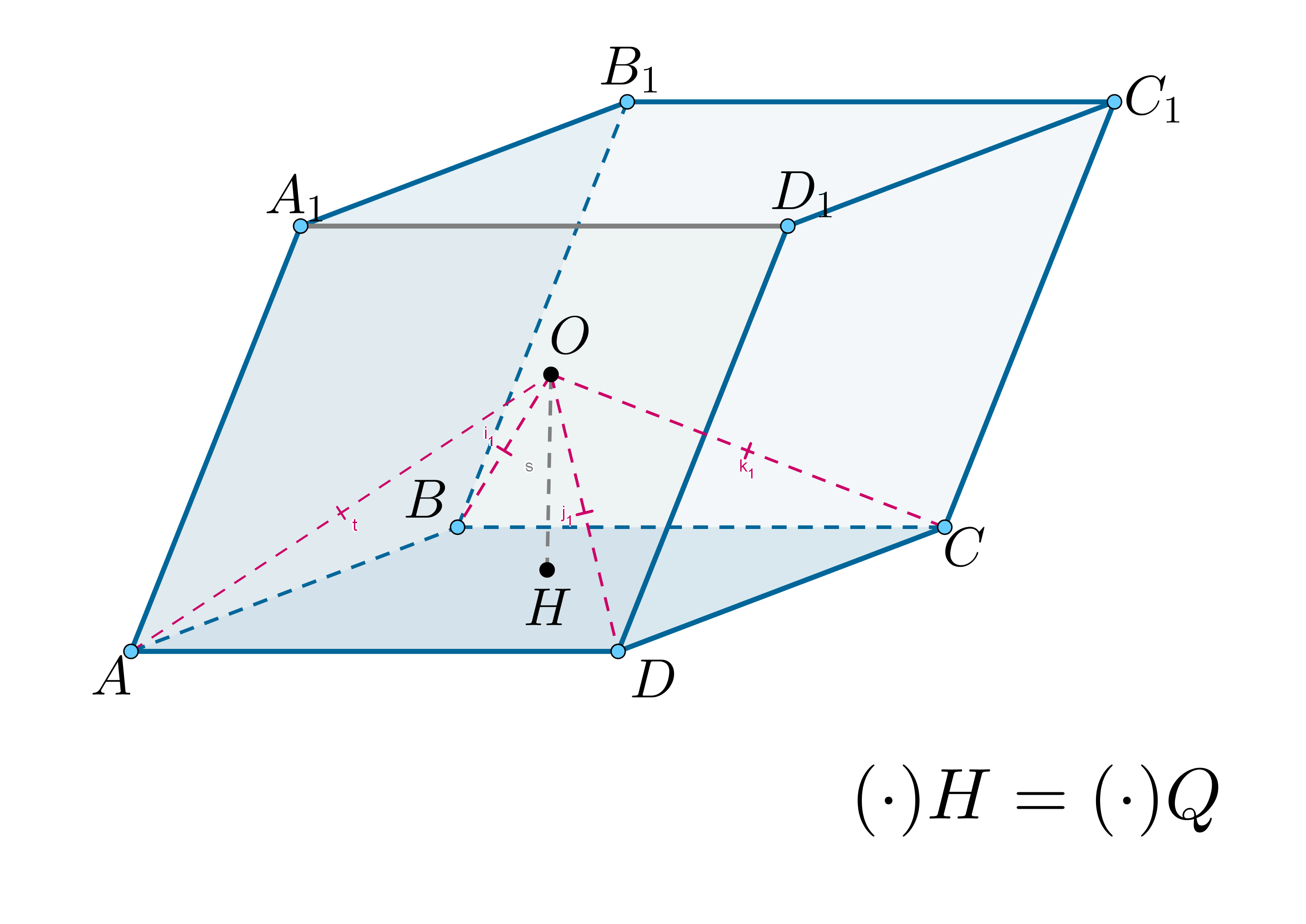
Все грани — прямоугольники. Рассмотрим прямую , где и — центры нижнего и верхнего оснований соответственно (точки пересечения диагоналей). параллельна боковым ребрам и перпендикулярна основаниям. Пусть — середина . Так как расстояния от точки до вершин равны, расстояния от до вершин равны, а также все эти расстояния равны между собой, имеем: треугольники как прямоугольные по двум катетам. Следовательно, гипотенузы равны, то есть расстояния от точки до всех вершин одинаковы. Значит, около него можно описать окружность.

Зааметим, что диагонали параллелепипеда пересекают в точке , следовательно, центр сферы, описанной около параллелепипеда есть точка пересечения его диагоналей, причем диагонали являются диаметрами сферы.

б) Обозначим ребра как , , , как показано на рисунке.

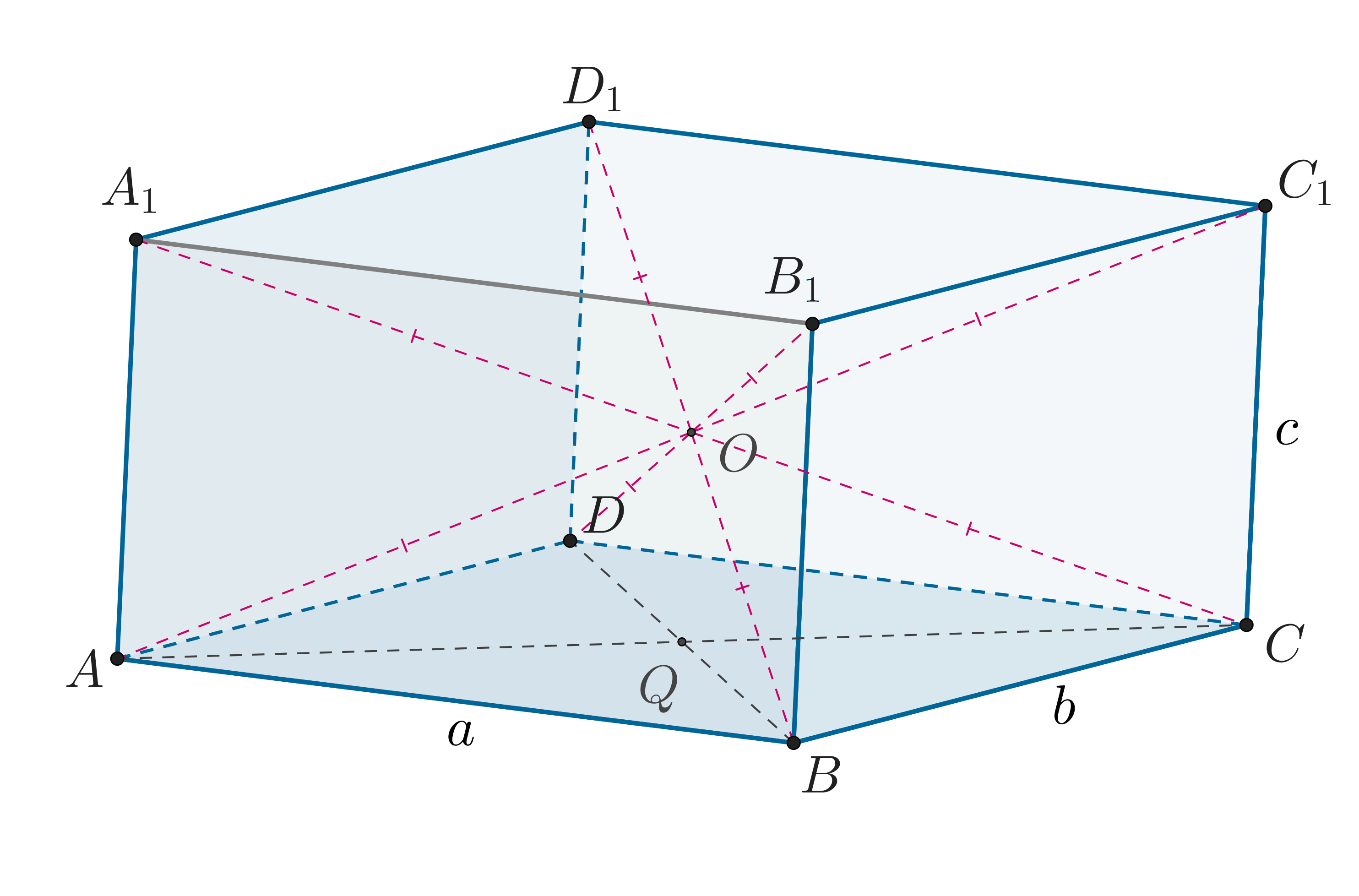
В пункте а) мы доказали, что точка пересечения диагоналей есть центр описанной сферы. Следовательно, половина диагонали параллелепипеда есть радиус этой сферы. То есть .

Нам требуется найти площадь полной поверхности , то есть выражение .

Известно, что , .

По неравенству о среднем

Равенство достигается тогда и только тогда, когда .

Следовательно,