14.04 Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус
Ошибка.
Попробуйте повторить позже
Шарик мороженого разрезали пополам. Из одной половинки шарика хотят
вырезать пирамидальную фигурку мороженого так, что основание этой
пирамиды лежит в круге сечения, вершина
лежит на поверхности шарика, а
объем такой пирамидальной фигурки наибольший.
а) Докажите, что объем пирамиды равен
где
— радиус
шарика мороженого.
б) Найдите если площадь треугольника
равна
где
— середины ребер
и
соответственно.
а) По формуле площади произвольного четырехугольника имеем:
Следовательно, если
— диаметры сферы и
то есть
Следовательно,
— квадрат.
Расстояние от точки до плоскости
наибольшее, если
и
— радиус сферы. Тогда объем пирамиды равен
Что и требовалось доказать.
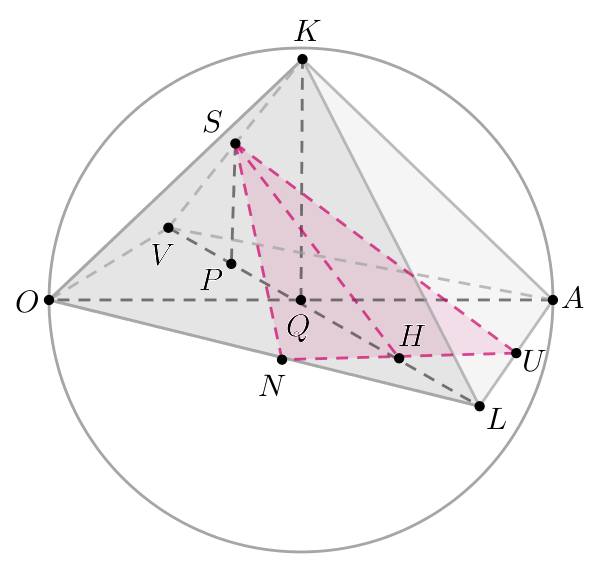
б) Проведем где
Тогда
и
Так как то
следовательно, по теореме о трех
перпендикулярах
где
Далее имеем:
Тогда по теореме Пифагора в треугольнике
Так как , то площадь треугольника
равна
б) 16
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




