.06 Гидростатика
Ошибка.
Попробуйте повторить позже
Изготовленная из соснового дерева тонкая прямая однородная палочка объёмом закреплена за свой верхний конец на
горизонтальной оси, вокруг которой она может вращаться в вертикальной плоскости. К нижнему концу этой палочки на тонкой
лёгкой нити привязан алюминиевый шарик. Шарик и нижняя часть палочки погружены в сосуд с водой, причём ниже уровня воды
располагается ровно половина палочки, и шарик не касается дна сосуда.
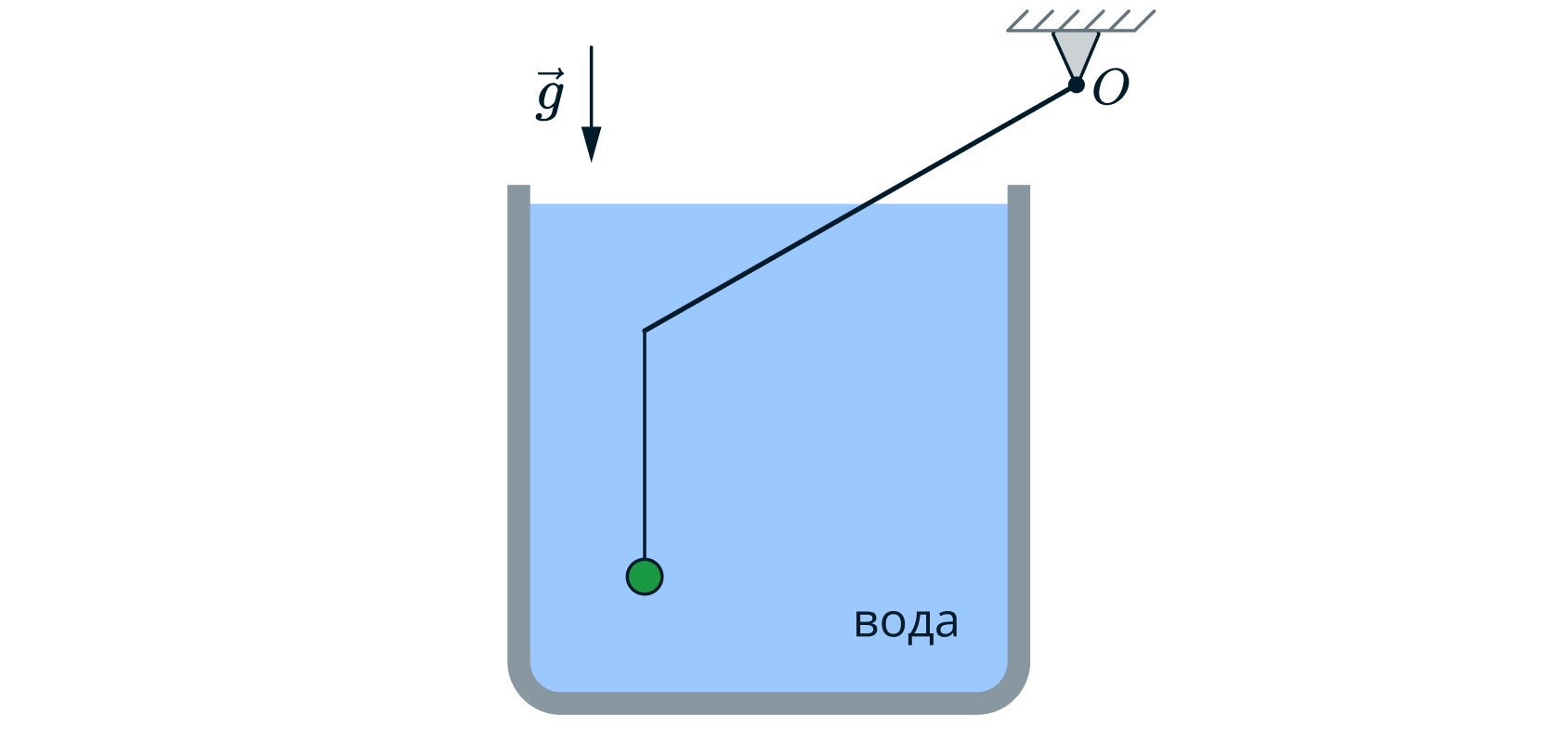
При этом палочка наклонена под некоторым углом к горизонту, и вся система находится в равновесии. Сделайте рисунок с
указанием сил, действующих на палочку и на шарик. Найдите объём шарика. Обоснуйте применимость используемых законов к
решению задачи.
Обоснование
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО).
2. Будем считать палочку абсолютно твёрдым телом. Условие равновесия твёрдого тела, которое может вращаться вокруг некоторой оси – равенство нулю суммы моментов всех сил, приложенных к телу, относительно этой оси. Груз будем описывать моделью материальной точки, его размерами можно пренебречь. Груз находится в покое относительно поступательного движения, следовательно, сумма сил, действующих на него, равна нулю.
3. Палочка тонкая, поэтому объём погруженной в воду части палочки можно считать прямо пропорциональным длине этой части.
4. Нить тонкая, поэтому можно пренебречь действующей на неё силой Архимеда.
5. Нить лёгкая, поэтому модуль силы натяжения нити в любой её точке одинаков, в частности: (см. рисунок в
решении).
6. Груз не касается дна сосуда, поэтому на него со стороны этого дна не действует сила реакции.
Решение
Изобразим силы, действующие на тела.
.png)
На шарик действует сила тяжести , где
– масса шарика, сила Архимеда
и сила натяжения нити
. На палочку
действует сила тяжести
, где
– масса палочки сила Архимеда
, сила натяжения нити
и сила реакции опоры
.
Запишем второй закон Ньютона для шарика
где – ускорение шарика.
Сила Архимеда равна
где – плотность жидкости,
.
Тогда
Массы тел равны
где – плотность алюминия,
– плотность соснового дерева.
Спроецируем второй закон Ньютона на ось :
С учётом уравнений для массы и силы Архимеда
Пусть длина палочки равна , и составляет угол
с горизонталью (см. рис.). Запишем правило момента для палочки
относительно оси вращения
, с учётом, что сила тяжести приложена в центре палочки, а сила Архимеда в центре погруженной
части палочки:
Учтем равенства для массы и силы Архимеда
Объединим (1) и (2)
Отсюда
| Критерии оценивания выполнения задачи | Баллы |
| Критерий 1 | |
| Верно обоснована возможность испольования законов | 1 |
| (закономерностей). В данном случае: выбор ИСО, модель материальной точки, модель абсолютно твёрдого тела, применение второго закона Ньютона, правила моментов, равенство модулей сил натяжения нитей | |
| В обосновании возможности использования законов | 0 |
| (закономерностей) допущена ошибка | |
|
ИЛИ
| |
| Обоснование отсутствует | |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы: | 3 |
| I) записаны положения теории и физические законы, | |
| закономерности, применение которых необходимо для решения | |
| задачи выбранным способом (в данном случае - правило моментов, формула момента силы, формула силы Архимеда, второй закон Ньютона, формуал связи массы, плотности и объема); | |
| II) описаны вновь вводимые в решении буквенные обозначения | |
| физических величин (за исключением обозначений констант, | |
| указанных в варианте КИМ, обозначений величин, используемых | |
| в условии задачи, и стандартных обозначений величин, | |
| используемых при написании физических законов); | |
| III) проведены необходимые математические преобразования | |
| и расчёты (подстановка числовых данных в конечную формулу), | |
| приводящие к правильному числовому ответу (допускается решение | |
| «по частям» с промежуточными вычислениями); | |
| IV) представлен правильный ответ с указанием единиц измерения | |
| фиизческой величины | |
| Правильно записаны все необходимые положения теории, | 2 |
| фиизческие законы, закономерности, и проведены необходимые | |
| преобразования, но имеется один или несколько из следующих | |
| недостатков. | |
|
| |
| Записи, соответствующие пункту II, представлены не в полном | |
| объёме или отсутствуют. | |
|
И(ИЛИ)
| |
| В решении имеются лишние записы, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения и не | |
| зачёркнуты | |
|
И(ИЛИ)
| |
| В необходимых математических преобразованиях или вычислениях | |
| допущены ошибки, и(или) в математических преобразованиях/ | |
| вычислениях пропущены логически важные шаги. | |
|
И(ИЛИ)
| |
| Отсутствует пункт IV, или в нём допущена ошибка (в том числе | |
| в записи единиц измерений величины) | |
| Представлены записи, соответствующие одному из следующих | 1 |
| случаев. | |
| Представлены только положения и формулы, выражающие | |
| физические законы, применение которых необходимо для решения | |
| данной задачи, без каких-либо преобразований с их | |
| использованием, направленных на решение задачи. | |
|
ИЛИ
| |
| В решении отсутствует ОДНА из исходных формул, необходимая | |
| для решения данной задачи (или утверждение, лежащее в основе | |
| решения), но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи. | |
|
ИЛИ
| |
| В ОДНОЙ из исходных формул, необходимых для решения данной | |
| задачи (или в утверждения, лежащем в основе решения), допущена | |
| ошибка, но присутствуют логически верные преобразования | |
| с имеющимися формулами, направленные на решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




