Тема . Механика. Кинематика

.06 Равноускоренное движение

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела механика. кинематика

Решаем задачу:

Ошибка.
Попробуйте повторить позже

Задача 1#22199

Поезд метро проходит расстояние $S$ между станциями, разгоняясь с ускорением $a$ до середины перегона и тормозя с таким же по модулю ускорением на второй половине пути. В какой момент времени $τ$ от начала движения средняя скорость $u-$ поезда на пройденном участке пути максимальна? Найдите это максимальное значение $u- max$ и расстояние $l$ от начала пути, на котором оно достигается.

(Всеросс., 2005, финал, 9)

Источники: Всеросс., 2005, финал, 9

Показать ответ и решение

Способ I
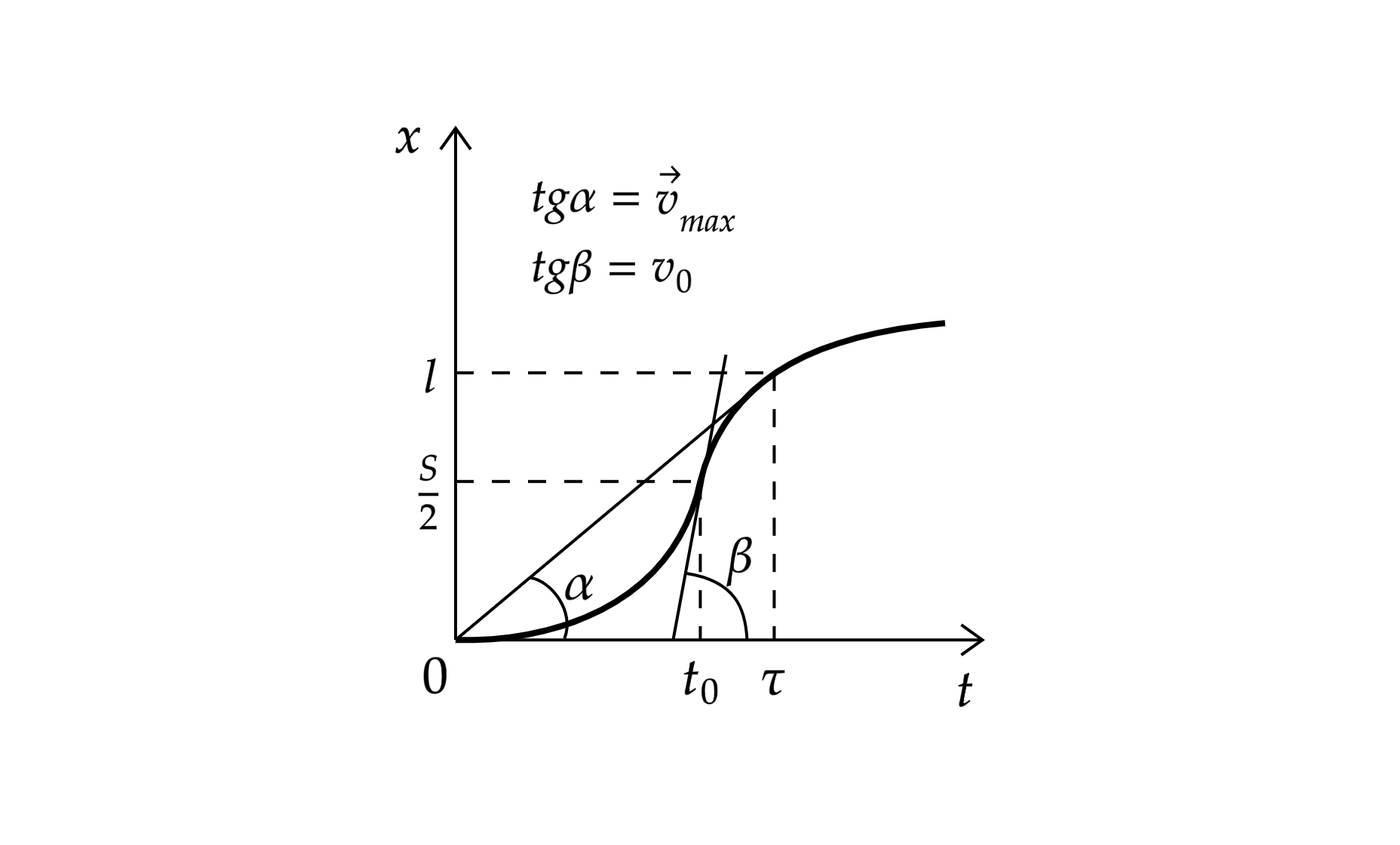
График зависимости координаты $x$ поезда от веремени $t$ представлен на рисунке. Средняя скорость $u(t)$ на участке пути, пройденном к моменту времени $t$ , равна угловому ускорению $x(t) k(t) = t$ прямой, проходящей через точку ( $t;x(t)$ ) и начало координат. Из графика видно, что $umax$ соответствует прямой, касающейся кривой $x(t)$ в точке ( $τ;l$ ).

Поезд проходит расстояние $S- 2$ от станции отправления за время $∘ -- t0 = S- a$ . Зависимость $x(t)$ для $t > t0$ имеет вид:

x(t) = S-+ at(t− t )− a(t− t )2. 2 0 0 2 0

С другой стороны,

x(τ) = umaxτ.

Подставляя (2) в (1), получаем

1 2 3 2 S- 2aτ + (umax − 2at0)τ + 2at0 − 2 = 0

Поскольку при $t = τ$ прямая $x = umaxt$ касается графика квадратичной функции $x(t)$ , дискриминант (3) должен быть равен нулю:

(u − 2at)2 − 3a2t2+ aS = 0, откуда u = √aS-(2± √2-) max 0 0 max

В последней формула следует оставить только знак «–», поскольку $umax$ не может превышать максимальной за все время движения скорости поезда $√ --- v0 = at0 = aS$ . Подставив $umax$ в (3), найдем $∘ --- τ = 2S- a$ . Искомое расстояние $√ - l = umax τ = 2S( 2− 1) ≈ 0,83S$
Способ II
Разделим наш путь до $τ$ на 2 составляющие, до $S- 2$ и от $S- 2$ до $τ$ .
Пусть первый участок поезд проезжает за время $t0$ , тогда скорость в конце первого участка пути равна

v = at0 (1)

Путь за время $t 0$ равен $S- 2$ , откуда время пути

∘ -- S-= at20 ⇒ t = S- (2) 2 2 0 a

Пусть время на втором участке равно $t1$ Время всего пути равно $τ$ оно будет складываться из $t0$ и $t1$ , значит $t1 = τ − t0$ После прохождения точки $S- 2$ поезд начинает тормозить, а его скорость уменьшаться по закону

v1 = at0 − at1 (3)

Наш путь от $t0$ до $τ$ равен

at21 L1 = at0t1 −-2 (4)

Но средняя скорость продолжает расти до момента, пока мгновенная скорость не станет равна средней скорости, найдем этот момент c учетом (1), (2), (3) и (4)

2 S-+ at1 + a(τ −-t0)- L-= v1 ⇒ 2-----------2-----= at0 − at1 τ τ

или

∘ -- S- √ --- √--- S- at20 2at0τ aτ2 2 + τ aS − aS ⋅ a − 2 + 2 − 2 = (at0 − aτ + at0)τ

Расскроем все и приведем подобные

S- √ --- S- √ --- aτ2 √ --- 2 √--- 2 + τ aS − S − 2 + τ aS − 2 = τ aS − aτ + τ aS

Выразим отсюда время

aτ2 ∘ 2S- − S = −--- ⇒ τ = --- 2 a

Найдем максимальную среднюю скорость

∘ --- u = 2√aS-− a 2S-= √aS-(2− √2-) max a

И расстояние

∘ 2S√ --- √ - √ - L = umaxτ = --- aS(2− 2) = 2S( 2− 1) a

Ответ:

Нужна консультация? Задайте нам вопрос в чате.

Специальные программы

Все специальные программы

Программа
лояльности v2.0

Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!

Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение

Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты

Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей

Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ

Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!

Программа
лояльности v2.0

Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!

Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение

Налоговые вычеты

Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ

Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!

.06 Равноускоренное движение

Специальные программы

Программалояльности v2.0

Крути рулеткуи выигрывай призы!

Бесплатное онлайн-обучение

Налоговые вычеты

Специальное предложениедля учителей

Вернём деньги за курсза твою сотку на ЕГЭ

Программалояльности v2.0

Крути рулеткуи выигрывай призы!

Бесплатное онлайн-обучение

Налоговые вычеты

Специальное предложениедля учителей

Вернём деньги за курсза твою сотку на ЕГЭ

Программа
лояльности v2.0

Крути рулетку
и выигрывай призы!

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ

Программа
лояльности v2.0

Крути рулетку
и выигрывай призы!

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ