.06 Равноускоренное движение
Ошибка.
Попробуйте повторить позже
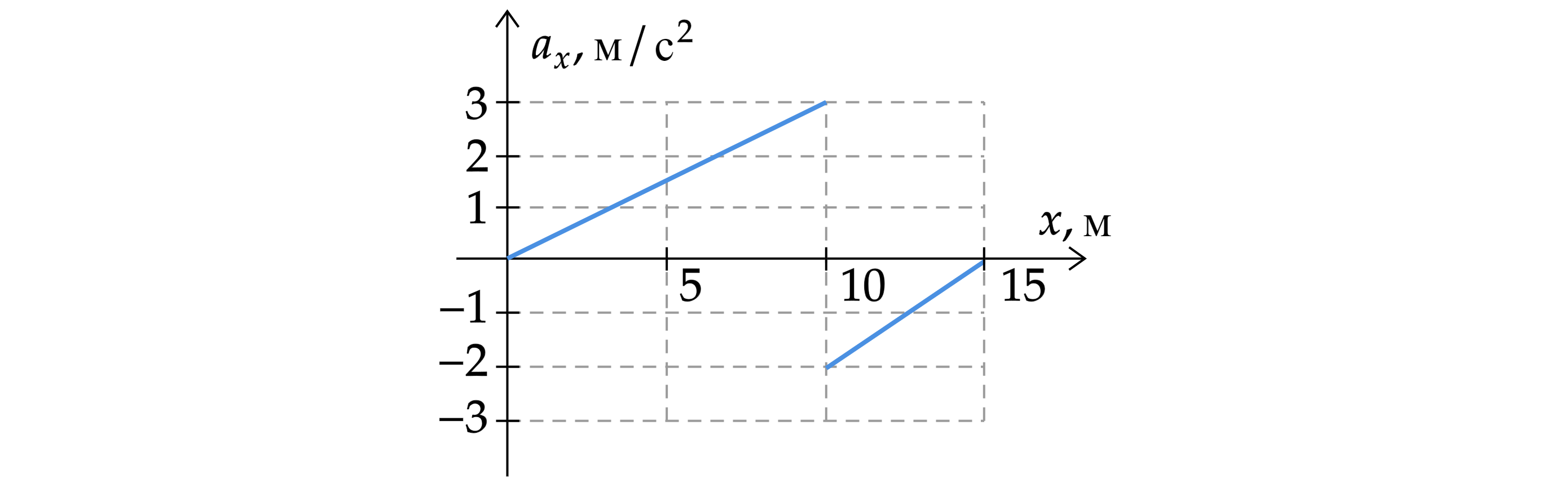
Тело движется в положительном направлении оси с ускорением, график зависимости которого от координаты тела
показан на рисунке. Найти скорость тела в тот момент времени, когда его координата равнялась
, если начальная
координата тела равнялась нулю, а начальная скорость –
(«Росатом», 2019, 11)
Источники:
Рассматриваемое движение не является равноускоренным. Мысленно разобьем перемещение тела на малые элементы
,
, ... настолько малые, что движение на каждом можно считать равноускоренным. Тогда для
– ого элемента
имеем
где и
– скорость тела в конце и в начале элемента,
– проекция ускорения тела на ось
внутри этого
элемента. Складывая такие равенства для каждого элемента, найдем
где и
– скорость тела в начале и в конце нашего движения. Сумма в скобках в правой части имеет смысл
площади под графиком зависимости проекции ускорения от координаты. Вычисляя эту площадь (по графику, используя
пропорциональные соотношения), получим
Отсюда
(Официальное решение Росатом)
| Критерии оценивания выполнения задачи | Баллы |
| Движение мысленно разбито на малые участки, такие, что внутри каждого движение можно считать равноускоренным | 0.5 |
| Для каждого малого участка найдена разность квадратов начальной и конечной скоростей | 0.5 |
| Определено, что сумма таких разностей определяет разность квадратов скоростей в начале и в конце рассматриваемого этапа движения | 0.5 |
| Получен правильный ответ | 0.5 |
| Максимальный балл | 2 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




