.02 Гравитация
Ошибка.
Попробуйте повторить позже
Исследовательский зонд.
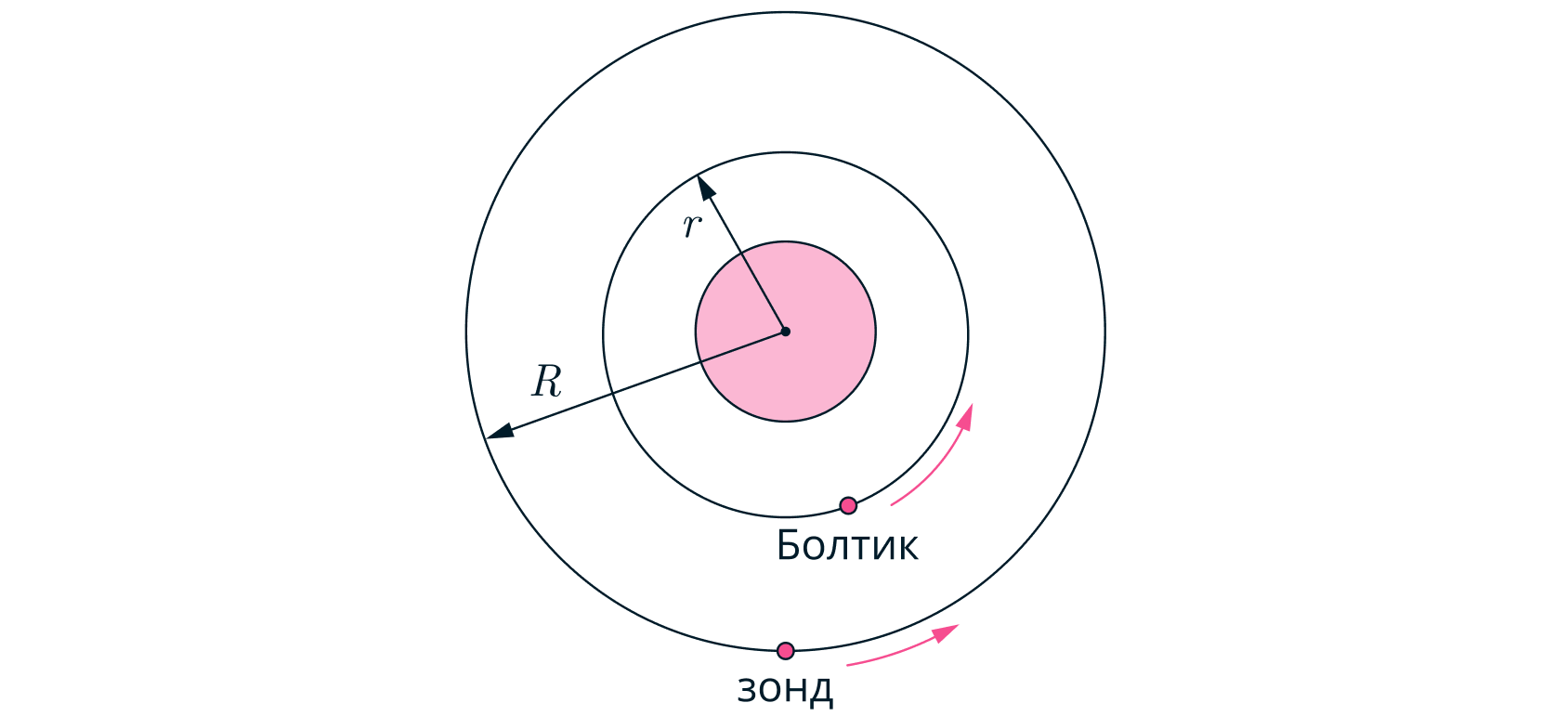
Исследовательский зонд, находящийся на круговой орбите радиуса вокруг планеты Шелезяка,
изучает движение Болтика — маленького спутника планеты. Орбита Болтика также является круговой
с радиусом
и лежит в той же плоскости, что и орбита зонда (см. рис.). В процессе
наблюдения приборы зонда зафиксировали, что Болтик спустя
мин после пересечения им
видимого края диска планеты оказался на максимальном угловом расстоянии
от центра
Шелезяки, а ещё спустя некоторое время, большее
, снова пересёк край видимого диска планеты.
Известно, что между указанными пересечениями других пересечений Болтика с видимым краем планеты
не было. Планета Шелезяка имеет форму шара и лишена атмосферы. Масса Болтика много
меньше массы планеты, зонд и спутник обращаются вокруг планеты в одну и ту же сторону.
Угловой диаметр планеты, наблюдаемый зондом, равен
. Гравитационная постоянная
.
1. Определите отношение .
2. Чему равен период обращения зонда вокруг Шелезяки?
3. Найдите среднюю плотность Шелезяки .
Примечания.
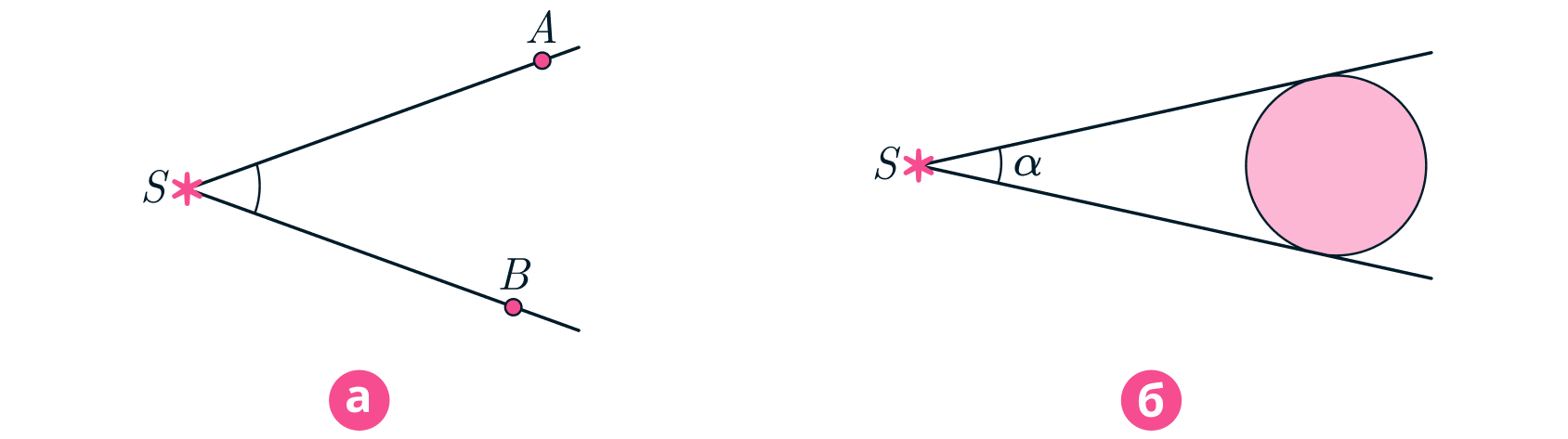
1. Угловым расстоянием между точками и
называется величина угла
, на сторонах
которого лежат рассматриваемые точки, а вершина
находится в точке наблюдения (см. рис.
а).
2. Угловым диаметром астрономического объекта (например, звезды или планеты) называется величина
максимально возможного угла между двумя касательными к поверхности рассматриваемого объекта,
вершина которого находится в точке наблюдения
(см. рис. б).
Источники:
1) Перейдем в СО, вращающуюся с угловой скоростью зонда относительно центра планеты. В такой СО Болтик будет двигаться так, что угловое расстояние между зондом и Болтиком будет увеличиваться, но в некоторый момент Болтик изменит свое направление движения, и тогда угловое расстояние будет уменьшаться. Максимальное угловое расстояние будет достигаться в момент перехода между этими двумя фазами движения. В этот момент скорость Болтика будет направлена вдоль направления расстояния между зондом и Болтиком. Это будет касательная к орбите Болтика проведенная из точки, где находится зонд.
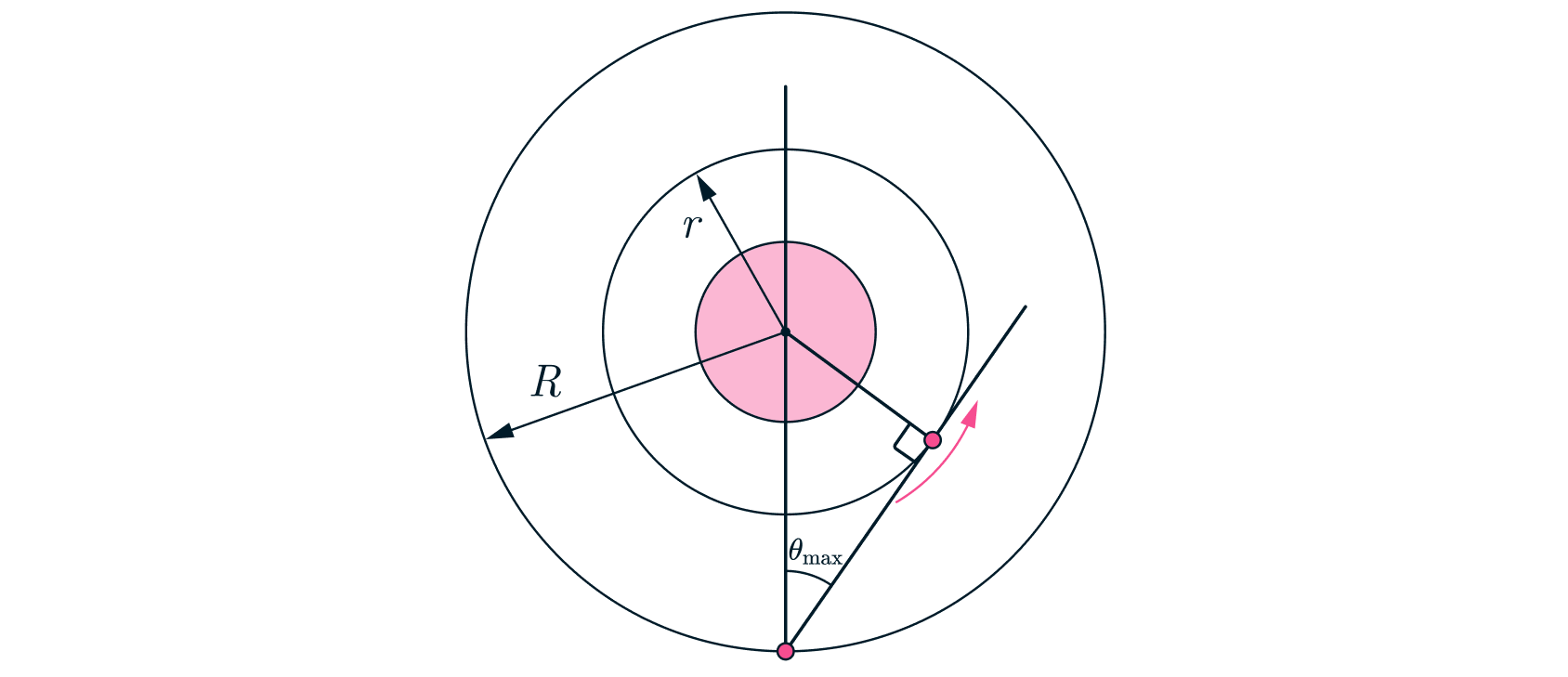
Из рисунка видим, что отношение можно выразить из получившегося треугольника.
Получим:
2) Запишем второй закон Ньютона для тела, которое двигается по орбите вокруг Шелезяки:
где - радиус орбиты.
Теперь распишем центростремительное ускорение:
И составим соотношение из уравнений такого вида записанных для Болтика и зонда:
Далее запишем угол, который пройдет за время Болтик. Это будет дуга между положением,
когда Болтик, зонд и край планеты находятся на одной прямой, и положением, когда болтик находится
на максимальном угловом расстоянии от центра планеты (способ поиска этой точки описан в пункте
1).
Получить такой угол можно перейдя в СО, вращающуюся с угловой скоростью зонда относительно
центра планеты. В такой СО угловая скорость Болтика:
Теперь запишем угол, который прошел Болтик:
На рисунке есть известные нам углы , а также искомый
.
Для начала рассмотрим . В нем распишем внешний угол как:
Угол можно найти из прямоугольного треугольника
:
Теперь найдем . Для этого выразим угол
по теореме синусов из треугольника
:
Так как искомый угол , то:
А угол в свою очередь:
Подставим найденнные значения в (3):
Вернемся к уравнению (2). В нем осталось выразить период обращения зонда используя (1):
3) Запишем второй закон Ньютона для зонда:
Теперь распишем центростремительное ускорение:
Выразим через известный нам период обращения зонда:
Затем распишем массу планеты через плотность и объем:
Выразим радиус Шелезяки через радиус орбиты зонда:
Подставим:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




