.15 Сила трения
Ошибка.
Попробуйте повторить позже
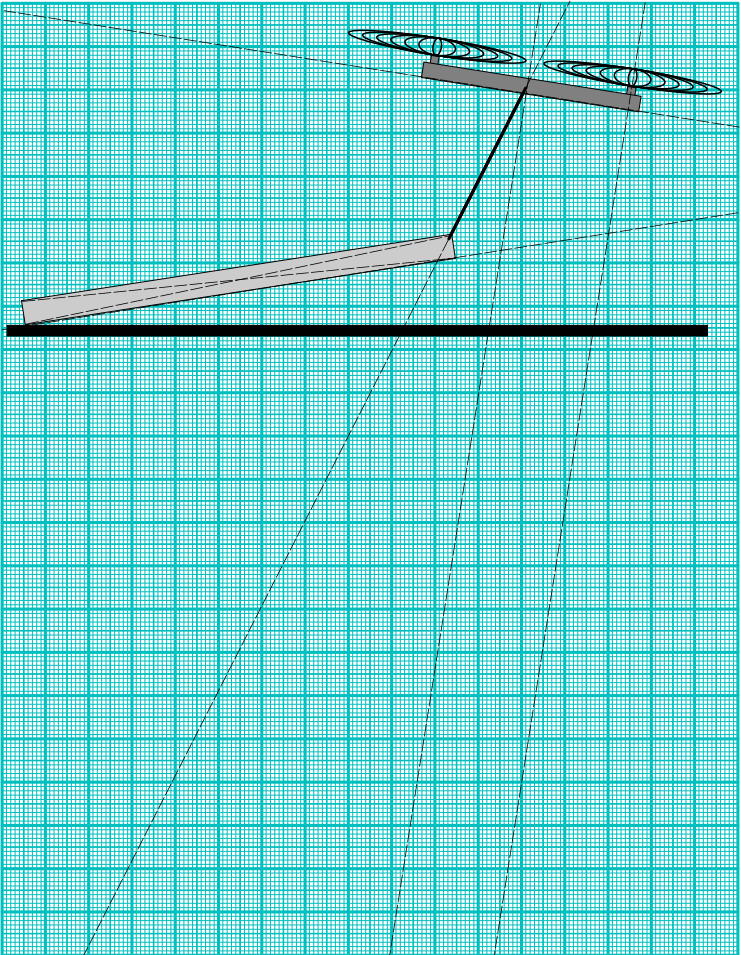
Дрон тянет брусок за нить, как показано на рисунке на отдельном листе. Брусок скользит с постоянной скоростью по горизонтальной поверхности. Брусок изготовлен из однородного материала. Можно проводить измерения на рисунке (на отдельном листе), считая, что размеры тел и расстояния соответствуют действительности с некоторым неизвестным масштабным коэффициентом. Если вы читаете условие с экрана, для вашего удобства на рисунке нанесены вспомогательные пунктирные линии (они могут быть полезны).
1. Найдите коэффициент трения между бруском и горизонтальной поверхностью.
2. Определите массу бруска, если масса дрона кг.
3. Теперь рассмотрим полет дрона в адиабатической атмосфере. В адиабатической атмосфере при смещении порции
воздуха по вертикали изменение ее параметров происходит по адиабатическому закону. Можно показать, что в такой
атмосфере температура является линейной функцией высоты :
, где
К - температура у
поверхности,
Дж/г
К - удельная теплоемкость воздуха при постоянном давлении, и
. Найдите
зависимость плотности воздуха
от высоты. Ответ выразите через плотность
у поверхности (на высоте
), удельную теплоемкость воздуха при постоянном объеме
Дж/г
, и определенные ранее
величины.
4. Считая, что максимальная высота полета дрона без нагрузки ограничивается мощностью его двигателей, найдите
Известно, что мощности двигателей хватает лишь для того, чтобы приподнять от поверхности нагрузку равную
массы дрона. Влиянием турбулентных эффектов на тягу двигателя можно пренебречь.
(NBPhO, 2020)
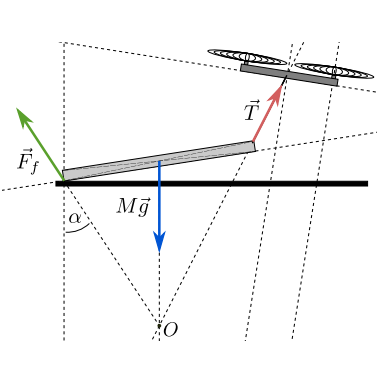
1. Пусть масса прямоугольного бруска равна M. На дрон действуют три силы: равнодействующая силы трения и
нормальной реакции , натяжение верёвки
, направленное вдоль верёвки, сила тяжести
, направленная
вертикально вниз из центра бруска.
Поскольку брусок скользит с постоянной скоростью, эти три силы должны уравновешивать друг друга. Единственный
способ, при котором это возможно - если векторные продолжения всех трёх сил пересекаются в одной точке . Это
можно доказать от противного: если силы не пересекаются в одной точке, рассмотрев момент сил относительно
любой точки пересечения двух сил, мы увидим ненулевой вращающий момент, что означает отсутствие
равновесия.
Если нормальная сила равна , то сила трения составляет
, поэтому равнодействующая:
Следовательно, всегда направлена под углом
к вертикали. Зная точки приложения и
направления сил тяжести и натяжения, можно определить положение точки
и
. Поскольку
,
коэффициент трения можно измерить как отношение горизонтальной и вертикальной составляющих
:
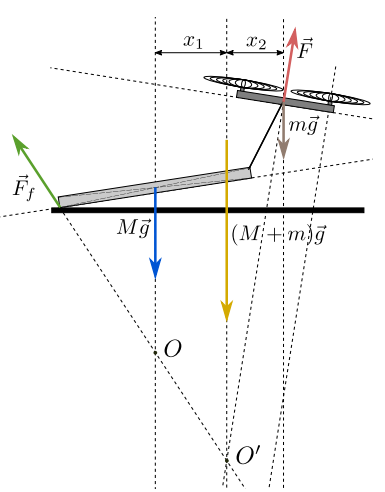
2. Рассмотрим систему, состоящую из бруска и дрона. На эту систему действуют три силы: cила тяжести ,
cила трения
, подъёмная сила
, удерживающая дрон в воздухе. Тяга дрона направлена вдоль его оси симметрии.
Поскольку система находится в равновесии, продолжения всех трёх сил должны пересекаться в одной точке .
Используя результаты предыдущей части, точку
можно найти как точку пересечения силы трения и подъёмной силы.
Так как сила тяжести действует вертикально, мы можем определить горизонтальное положение центра масс
системы. Если
и
- горизонтальные расстояния от
до центров масс бруска и дрона соответственно,
то:
Из измерений по рисунку получаем , следовательно:
3. Рассмотрим "карман"воздуха с фиксированной массой, движущийся в атмосфере. Пусть его объём . Для
адиабатической атмосферы:
где - показатель адиобаты. Поскольку
и
, получаем:
Следовательно:
4. Дрон поддерживает высоту за счёт работы двигателя, который прогоняет воздух через пропеллеры. Величина
тяги явно зависит от плотности воздуха и скорости
потока через пропеллеры. Уравнение баланса
сил:
где - вертикальная тяга,
- общая масса дрона. Если
- эффективная площадь пропеллеров, выражение
для
можно получить либо через динамическое давление
, либо из закона сохранения импульса. За время
через пропеллеры проходит объём воздуха:
Импульс этого объёма:
Следовательно, тяга:
Мощность двигателя связана с плотностью воздуха и скоростью потока. Лопасти пропеллера наклонены, что
создаёт крутящий момент, пропорциональный
. Скорость вращения лопастей пропорциональна
, поэтому выходная
мощность:
При постоянной мощности двигателя:
Из баланса сил следует:
Сравнивая значения на высотах и
:
Отсюда максимальная высота:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!