.15 Сила трения
Ошибка.
Попробуйте повторить позже
Однородный диск раскрутили вокруг его оси до угловой скорости и положили на границу раздела
двух горизонтальных полуплоскостей так, что его центр оказался точно на границе (см. рисунок; вид
сверху). Коэффициент трения между диском и одной полуплоскостью
, между диском и другой
полуплоскостью
. Найти ускорение центра диска сразу после того, как он оказался на
поверхности.
(«Росатом», 2019, 11)

Источники:
Мысленно разобьем диск на узкие колечки, найдем силу трения, действующую на каждое, а потом просуммируем. Рассмотрим четыре малых элемента кольца одинаковой длины, лежащих на одинаковых расстояниях от границы полуплоскостей на одной и второй полуплоскости (см. рисунок). На них действуют силы трения, направленные противоположно скорости элементов (т.е. по касательным к кольцу). Но поскольку коэффициенты трения диска о полуплоскости – разные, то две силы будут больше двух других, и суммарная сила трения не будет равняться нулю.
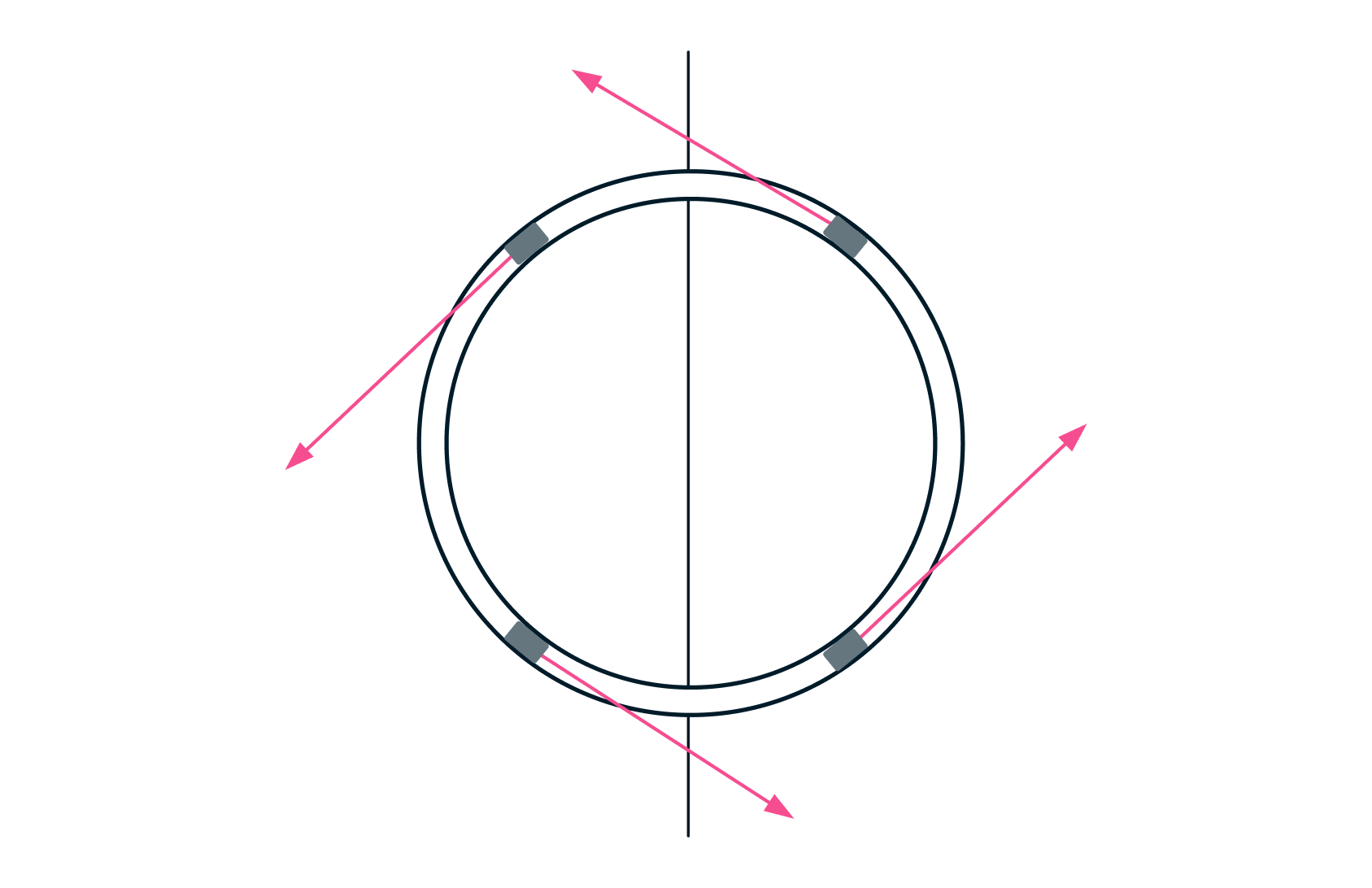
Рассмотрим силы, действующие на два таких элемента, лежащих на одной и той же полуплоскости. Очевидно, сумма сил трения, действующих на них, будет направлена вдоль границы и равна
где – коэффициент трения между диском и той полуплоскостью, на которой находятся
рассматриваемые элементы диска,
– масса каждого элемента,
– угол между элементами и
перпендикуляром к границе раздела между полуплоскостями (см. рисунок).
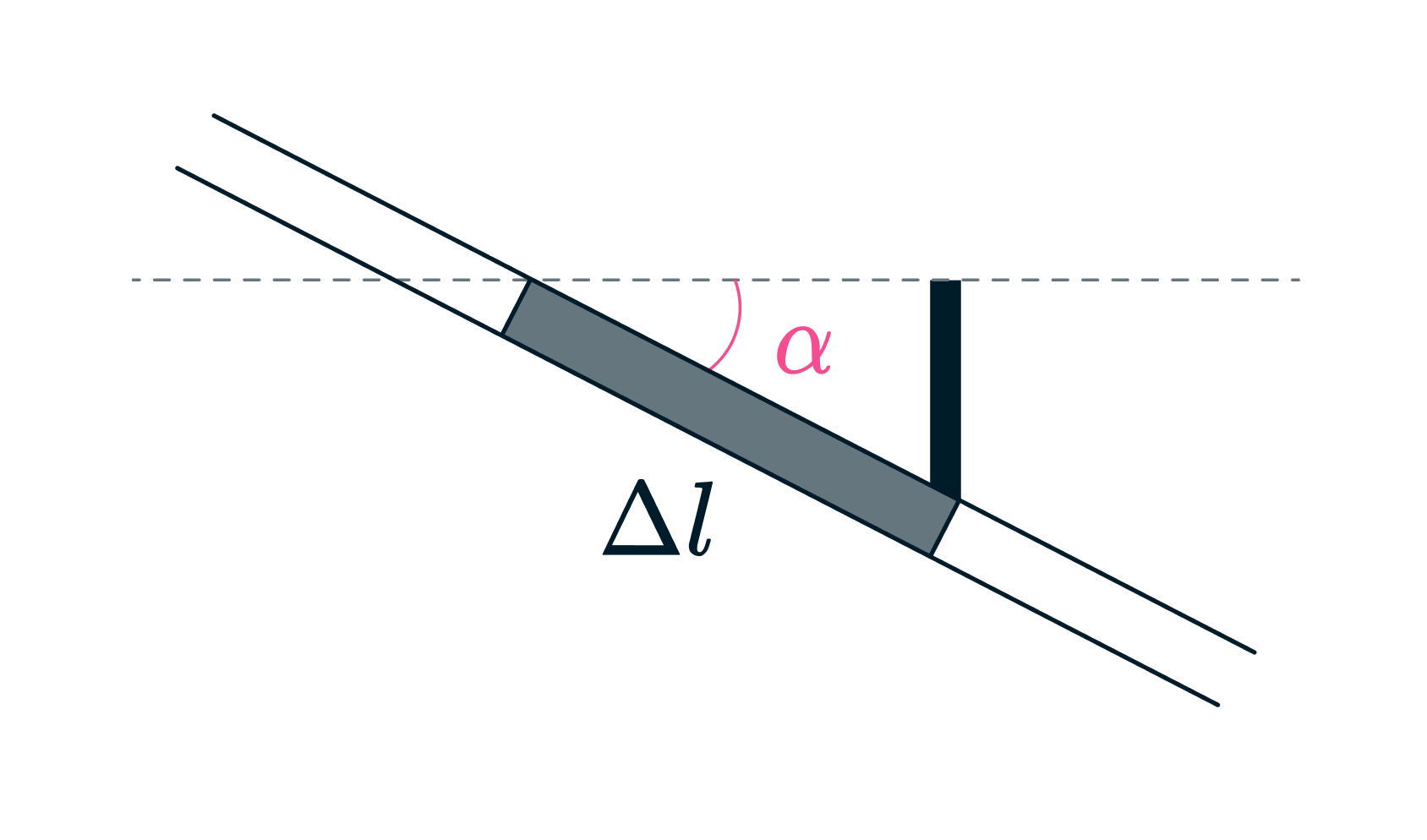
Масса элемента пропорциональна его длине
где – масса кольца,
– его длина,
– длина рассматриваемых элементов. Поскольку
величина
имеет смысл проекции рассматриваемого элемента кольце на границу раздела между полуплоскостями, то их сумма дает диаметр кольца. Поэтому сумма проекций сил трения, действующих на элементы кольца, находящихся с одной стороны от границы раздела дает
где – радиус рассматриваемого кольца. Сумма проекций сил трения, действующих на другую
половину дает
Поэтому суммарная сила трения, действующая на рассматриваемое кольцо, есть
Суммируя силы трения, действующие на отдельные колечки, найдем результирующую силу трения, действующую на диск
где – масса диска. Отсюда находим ускорение центра диска, которое будет направлено вдоль
границы полуплоскостей
Поэтому в рассматриваемом варианте ( ,
) имеем
(Официальное решение Росатом)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




