.15 Сила трения
Ошибка.
Попробуйте повторить позже
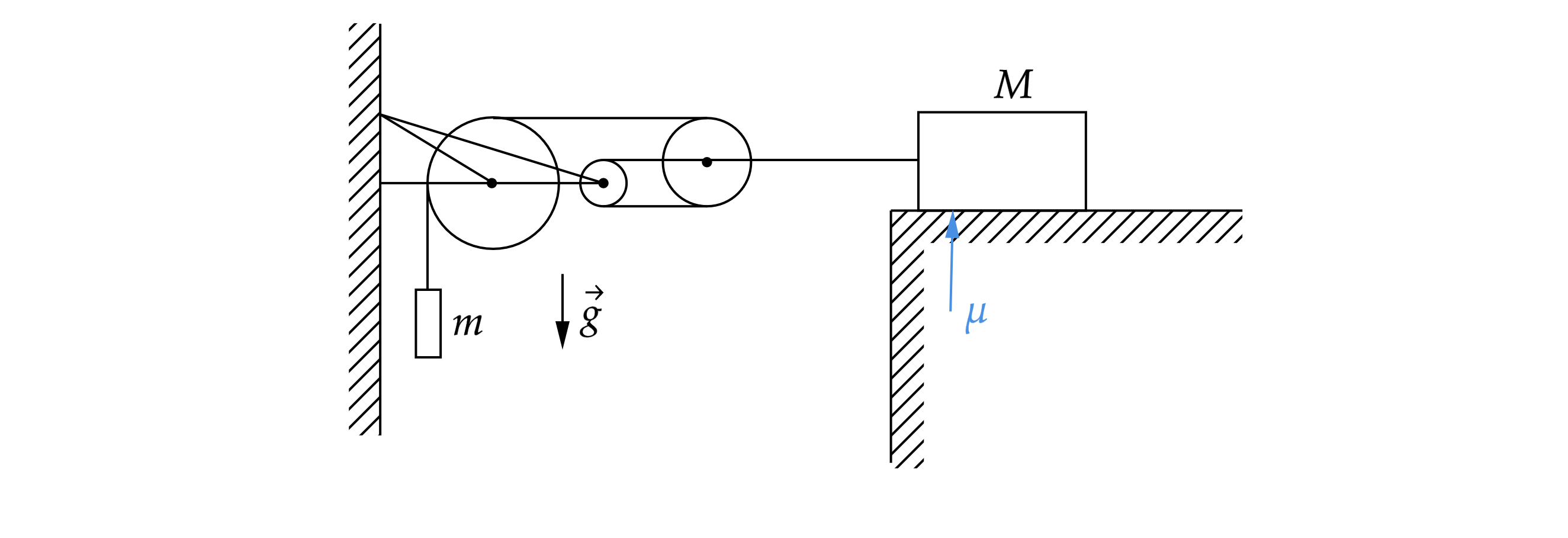
Экспериментатор Глюк обнаружил у себя в архивах чертеж механической системы, включающей в себя
грузы массой и
, три невесомых блока и невесомые нерастяжимые нити, причем трения в блоках
нет. Груз
висит вертикально, а груз
лежит на шероховатой горизонтальной плоскости. Найдите
ускорение груза
, считая, что
,
,
. Обратите внимание, что конец левой нити
прикреплен к оси самого правого блока и к этой же оси прикреплена другая нить, соединенная с грузом
.
(Всеросс., 2020, МЭ, 11)
Источники:
Для описания движения данной системы тел выберем неподвижную систему отсчёта, ось которой направлена
вертикально вниз, куда может двигаться грузик
, а ось
по горизонтали справа налево, в направлении возможного
движения груза массой
. Обозначим силу натяжения первой нити через
, а второй - через
(см.
рисунок).
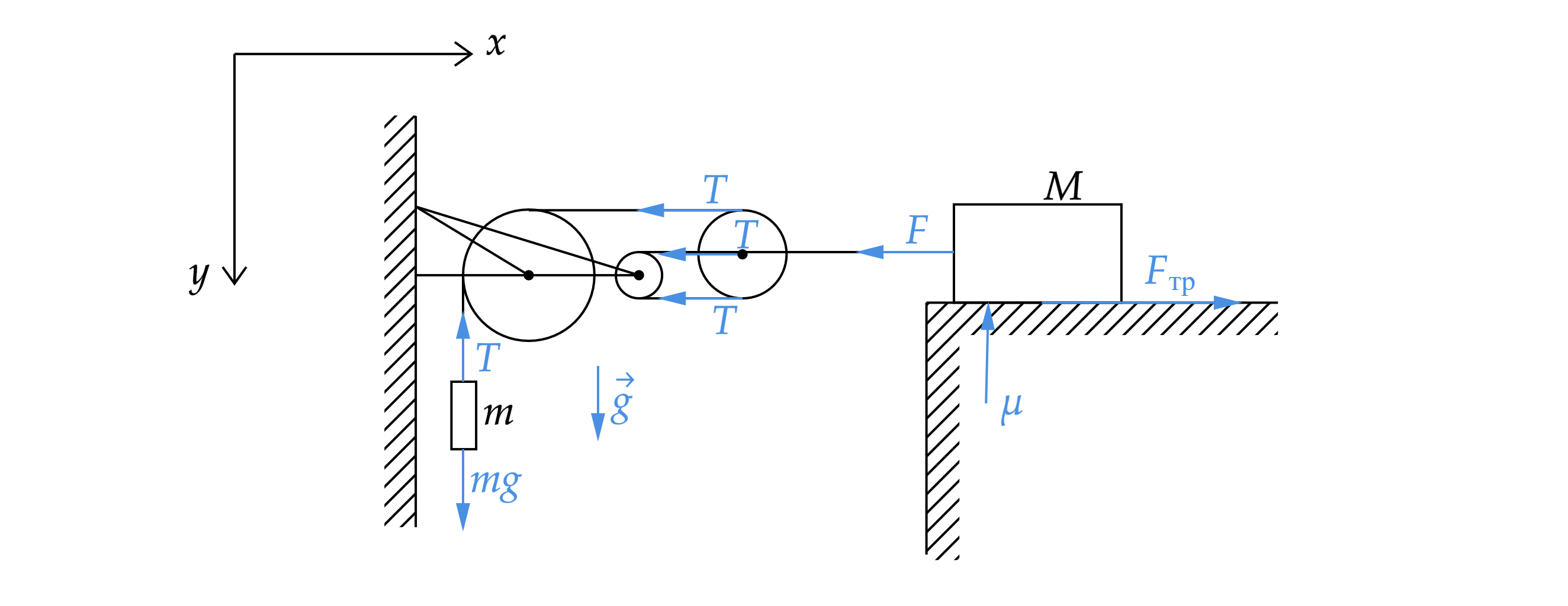
Тогда в проекциях на выбранные оси координат уравнение движения двух тел системы имеют вид:
В силу условия задачи можно считать, что сила натяжения вдоль всей первой нити одинакова и равна
, а сила натяжения второй нити
, так как для правого блока сумма сил должна быть равна
нулю.
Если груз сдвинется влево на расстояние
, то грузик
за счет укорочения трех горизонтальных участков
первой нити сдвинется вниз на расстояние
. Поэтому уравнение кинематической связи для ускорений тел имеет
вид:
. При движении данной системы тел если
, то на груз
действует сила трения
скольжения
Подставим в исходную систему уравнений все полученные выражения:
Отсюда:
тогда
Так как получено положительное значение ускорения, то тела действительно будут двигаться, поэтому предположение о действующей силе трения верно.
(Официальное решение ВсОШ)
| Критерии оценивания выполнения задачи | Баллы |
| Представлен рисунок с верно отмеченными силами и указанными осями | 1 |
| Записан второй закон Ньютона для каждого тела | 2 |
| Получена связь между | 1 |
| Получена и обоснована связь между ускорениями тел | 3 |
| Получено верное выражение для ускорения груза | 2 |
| Получен верный численный ответ | 1 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




