17.10 Медиана и удвоение медианы
Ошибка.
Попробуйте повторить позже
В равностороннем треугольнике провели медианы
и
На медиане
отметили точку
так, что
а) Докажите, что описанная вокруг треугольника окружность делит
отрезок
в отношении
считая от вершины
б) Известно, что эта же окружность пересекает в точке
Её радиусы
и
пересекают медианы
и
в точках
и
Найдите
отношение
а)
1. Пусть медианы пересекаются в точке
По свойству данной точки
2. Раз и
то
— это середина отрезка
3. По определению — это средняя линия
которая параллельна
4. Проведём высоту в
лежит на высоте треугольника
следовательно,
и
5. Продлим до пересечения с
в точке
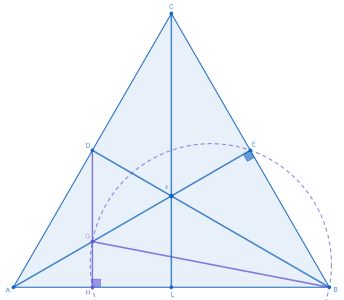
6. Поскольку и
— середина боковой стороны
то
— это
средняя линия
и
7. В равностороннем треугольнике высоты и медианы совпадают, стало быть,
— середина
откуда
8. Теперь нам осталось доказать, что — это и есть та самая точка
пересечения окружности и отрезка
(не считая точки
).
9. откуда
— вписанный и
—
действительно точка пересечения окружности с отрезком
Ч.Т.Д.
б)
1. Провед̈eм перпендикуляры и
на
и
соответственно.
2. Поскольку равносторонний, то
и
ещё и биссектрисы.
Таким образом,
3. По сумме углов
4. Вписанный и центральный
опираются на одну дугу, стало
быть
5. Поскольку то
—- вписанный и
6. как вертикальные.
то есть
7. поскольку
и
— перпендикуляры.
8. Из прошлых двух пунктов выводим подобие по двум
углам. Раз так, то
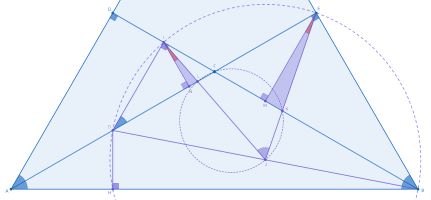
9. следовательно,
— диаметр и
10. и
— середина
стало быть
— средняя линия
11. Из прошлого пункта следует, что с коэффициентом
подобия
12.
Эти три тезиса в сумме
говорят о равенстве
13. Из прошлых двух пунктов следует, что с тем же
коэффициентом подобия
14. и
— высоты данных треугольников, следовательно, их длины
связаны тем же коэффициентом подобия
15. Из пунктов 14) и 8) следует, что
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




