.10 Наклонная плоскость
Ошибка.
Попробуйте повторить позже
Призма находится на горизонтальной поверхности шероховатого стола (см. рисунок). На поверхность призмы, наклонённую
под углом к горизонту, положили брусок массой
и отпустили. Он стал соскальзывать, а призма осталась в
покое. Коэффициент трения скольжения между бруском и призмой равен
. Найти силу трения между призмой
и столом. Какие физические законы Вы использовали при решении задачи? Обоснуйте их применение в данном
случае.

Источники:
Изобразим силы, действующие на призму и брусок. На брусок действует сила тяжести , нормальная сила реакции опоры
,
– сила трения со стороны призмы. На призму действует сила тяжести
, нормальная сила реакции
опоры со стороны стола
, вес бруска
, сила трения со стороны бруска
, сила трения со стороны стола
.
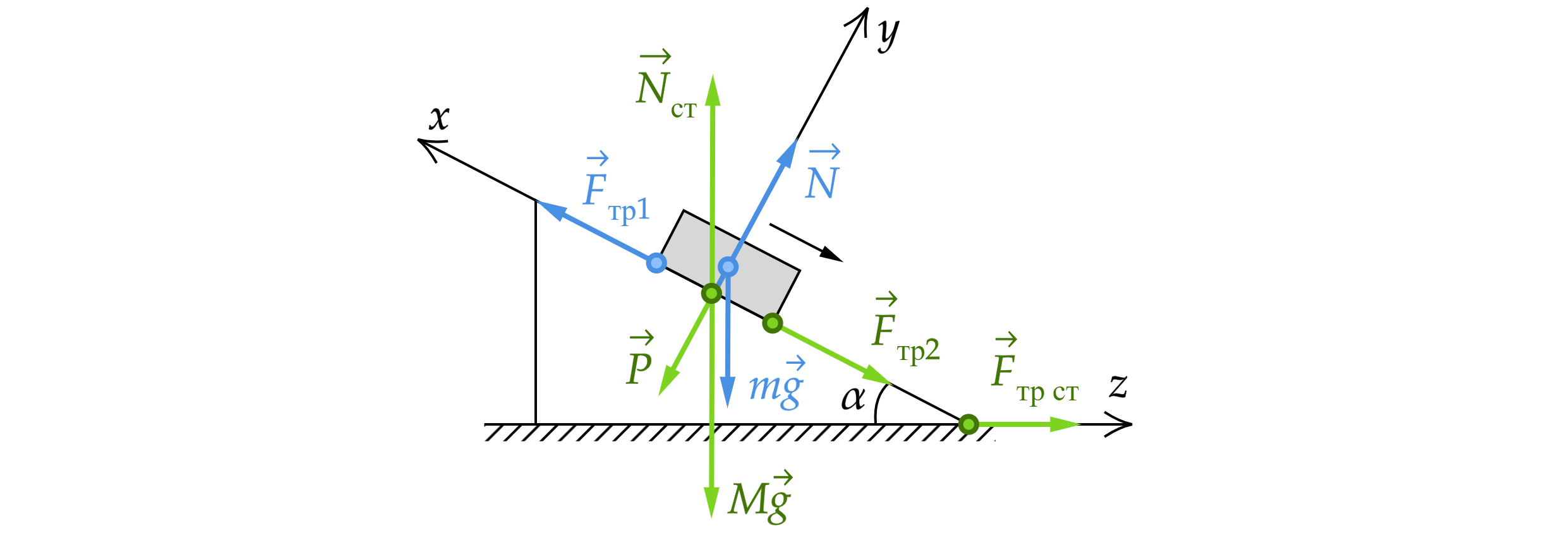
При этом, по третьему закону Ньютона ,
.
Запишем второй закон Ньютона для бруска
где – ускорение бруска.
Спроецируем на ось :
Сила трения же равна
Запишем второй закон Ньютона для призмы
где – масса призмы,
– ускорение призмы.
Так как призма покоится, то . Спроецируем второй закон Ньютона на ось
:
с учётом предыдущих уравнений
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




