.10 Наклонная плоскость
Ошибка.
Попробуйте повторить позже
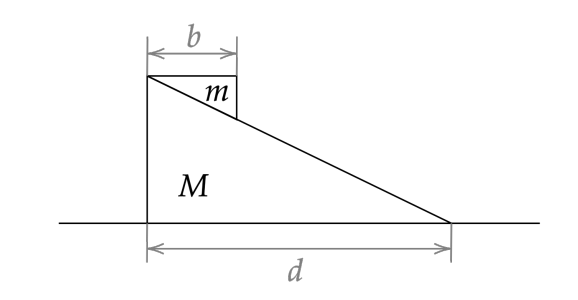
Какое расстояние пройдёт нижняя призма, когда верхняя коснётся плоскости? Размеры и массы тел указаны на
рисунке. В начальный момент система покоилась. Трения нет. Чему равен угол
между направлением вектора
абсолютной скорости верхней призмы и горизонталью, если наклонная поверхность нижней призмы образует с горизонтом
угол
(МОШ, 2017, 10)
Источники:
.png)
1. Расставим силы, действующие в системе «клин—шайба». Ускорение шайбы относительно клина направлено
вдоль его поверхности. При этом сам клин в процессе движения шайбы также смещается и преобретает
ускорение, направленное против движения шайбы горизонтально. Оба этих ускорения отметим на рисунке.
Тогда ускорение шайбы в инерциальной системе отсчета будет представлено векторной суммой ускорений
.
Замечание: закон сложения ускорений работает только в том случае, когда система движется поступательно.
2. Запишем 2ой закон Ньютона для клина и правило сложения ускорений в одной системе уравнений:
Введем координатные оси для клина и шайбы так, как показано на рисунке и спроецируем 2ой закон Ньютона на координатные оси:
Первое уравнение системы в проекции на оси
соответственно:
То же для клина (во второе уравнение следующей системы сразу подставим первое):
Теперь несложно выразить ускорение клина:
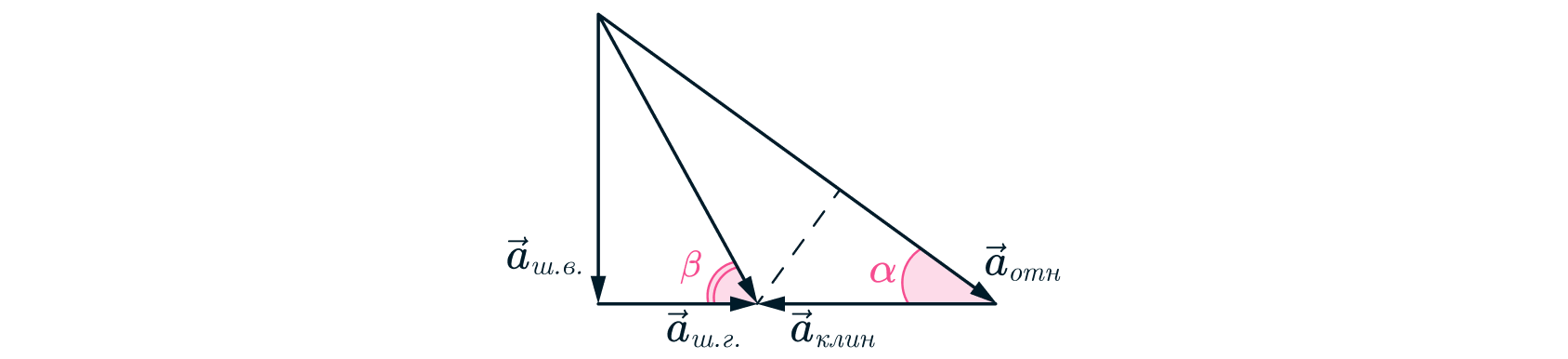
3. Введем компоненты ускорения шайбы: и
— горизонтальная и вертикальная соответственно. Вынесем их
на треугольнике ускорений и отметим соответствующий угол
который нужно найти в задаче:
Воспользуемся связью относительного и абсолютного ускорений шайбы и получим:
Тогда и
легко найти из треугольника ускорений:
Теперь выразим :
Окончательно получаем:
4. Осталось ответить на первый вопрос задачи:
Запишем выражения для перемещения призмы вдоль клина и перемещения клина
:
Отсюда
Из картинки: и окончательно получаем:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




