.10 Наклонная плоскость
Ошибка.
Попробуйте повторить позже
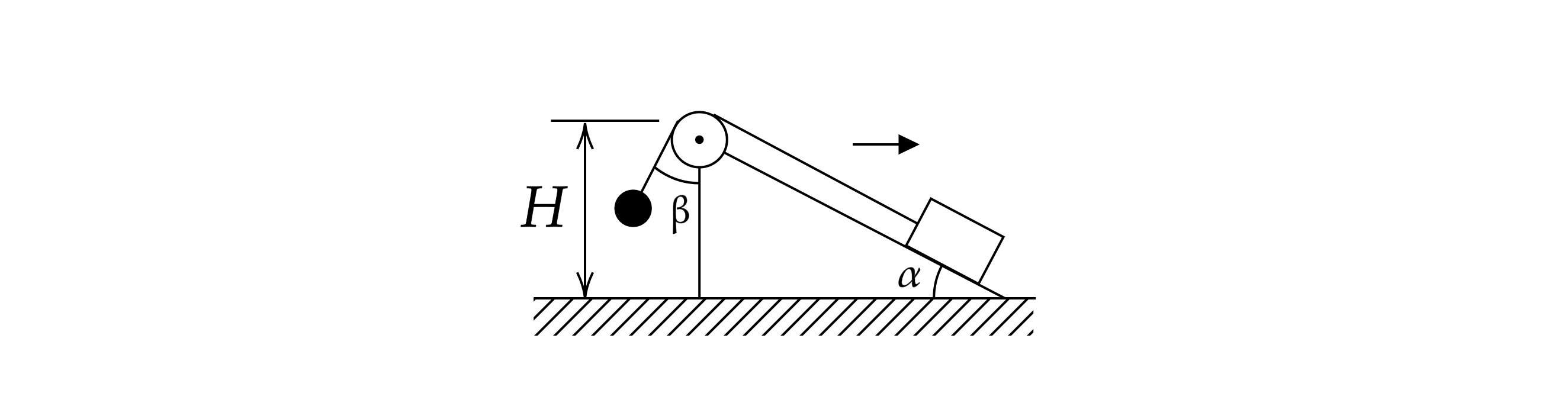
Клин с углом наклона (
) находится на горизонтальном столе. Через невесомый блок,
укрепленный на клине, перекинута легкая нерастяжимая нить, к концам которой привязаны шарик
массой
и брусок массой
(см. рис.). Вначале систему удерживают неподвижно, расположив
шарик вблизи блока на расстоянии
от стола, нить при этом не провисает. Затем клин стали
двигать с постоянным горизонтальным ускорением, а шарик отпустили. Брусок и шарик
пришли в движение, при этом нить, привязанная к шарику, составила угол
(
) с
вертикалью. Все точки системы перемещаются в вертикальной плоскости. Трением в оси
блока и бруска о клин пренебречь. Шарик достигает стола раньше, чем брусок доезжает до
блока.
1) Найти ускорение клина.
2) С каким ускорением относительно клина движется брусок?
3) Через какое время шарик достигнет стола?
(Физтех, 2021, 9)
Источники:
Заметим, что
Пусть – ускорение клина,
– ускорение бруска и шарика относительно клина,
– сила натяжения нити,
– сила давления клина на брусок,
,
(см.
рис.).
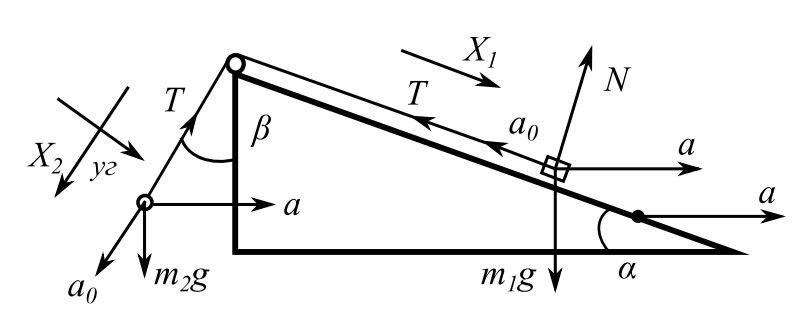
Так как клин и тело движутся неразрывно, то ускорение тела в системе отсчета клина будет
направлено вдоль плоскости клина и будет равно . Так как нить неразрывна и нерастяжима, то
ускорение шарика равно ускорениб бруска.
1) Ускорение шарика равно сумме переносного и его относительного
ускорений. Аналогично для
бруска. Уравнение движения для шарика в проекциях на ось
:
Отсюда
2) Уравнения движения для бруска в проекциях на ось :
Уравнения движения для шарика в проекциях на ось :
Отсюда с учетом выражения для находим:
3) Для шарика относительно стола в проекциях на вертикальную ось:
Отсюда
Время можно найти и в системе отсчета, связанной с клином.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




