Зачем делить в комбинаторике

Проведем через 2 вершины и центр квадрата прямые, параллельные осям, как на картинке.

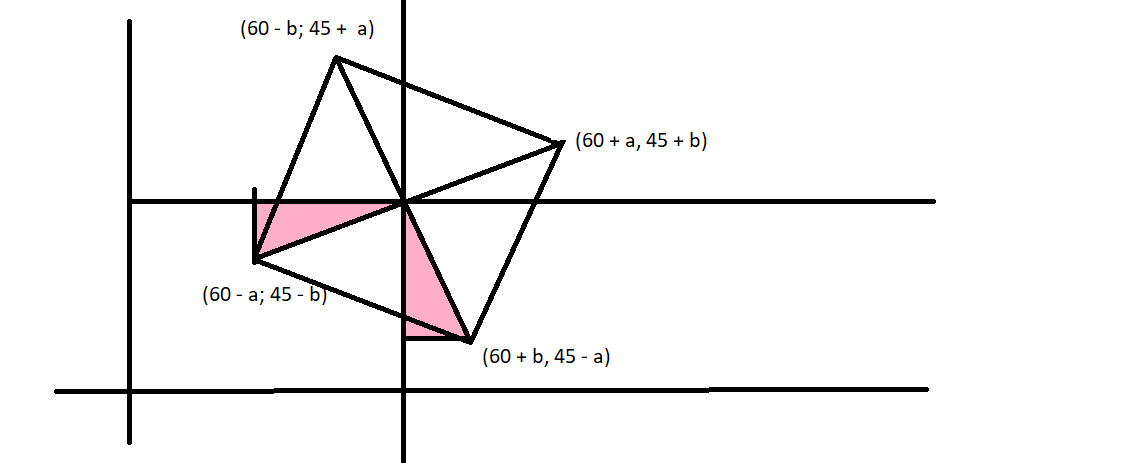
Заметим, что выделенные на картинке цветом треугольники равны по двум углам и стороне. Значит, если одна вершина с координатами , то следующая , затем по аналогичным соображениям следующая вершина и последняя . Тогда из условия, что все координаты неотрицательные получаем, что числа неотрицательны. Отсюда и . Значит, для значения у нас вариант и для значения у нас вариант, но если , то не получится квадрат. Итого: вариантов для пар , но заметим, что в квадрате изначальную вершину можно выбрать четырьмя способами. Значит, четырём парам значений и соответствует один квадрат. Таким образом, квадратов .