Медианы
Ошибка.
Попробуйте повторить позже
Серёжа нарисовал треугольник и провёл в нем медиану
Затем он сообщил Илье, какова в этом треугольнике длина
медианы
и какова длина стороны
Илья, исходя из этих данных, доказал утверждение: угол
тупой, а угол
острый. Найдите отношение
(и докажите для любого треугольника с таким отношением утверждение
Ильи).
Подсказка 1.
Для начала полезно построить контрпримеры к условию и найти, какие отношения при этом могут достигаться. Например, в условии идёт речь об угле CAB. Какое значение угла можно взять, чтобы он был близок к тупому, но всё же не тупым?
Подсказка 2.
Конечно же, прямой! Тогда точка A лежит на окружности с диаметром BC, AD является ее радиусом. Какие отношения может принимать отношение хорды AC к радиусу окружности?
Подсказка 3.
Любая хорда не длиннее диаметра, так что это отношение точно меньше двух. Итак, мы получили какую-то границу. Теперь попробуем доказать, что при отношении в точности 2 условие задачи выполняется.
Подсказка 4.
Медиана вдвое короче стороны, так что удвоением медианы можно получить равнобедренный треугольник. Тогда нетрудно заметить, что требуемые углы как раз получаются острым и тупым.
Подсказка 5.
Теперь осталось построить контрпример для отношения, большего двух. Для этого можно попробовать взять за прямой угол, который должен быть острым.
Подсказка 6.
Чтобы получить нужное неравенство, снова полезно удвоить медиану. Теперь осталось вспомнить, что против большего угла лежит большая сторона.
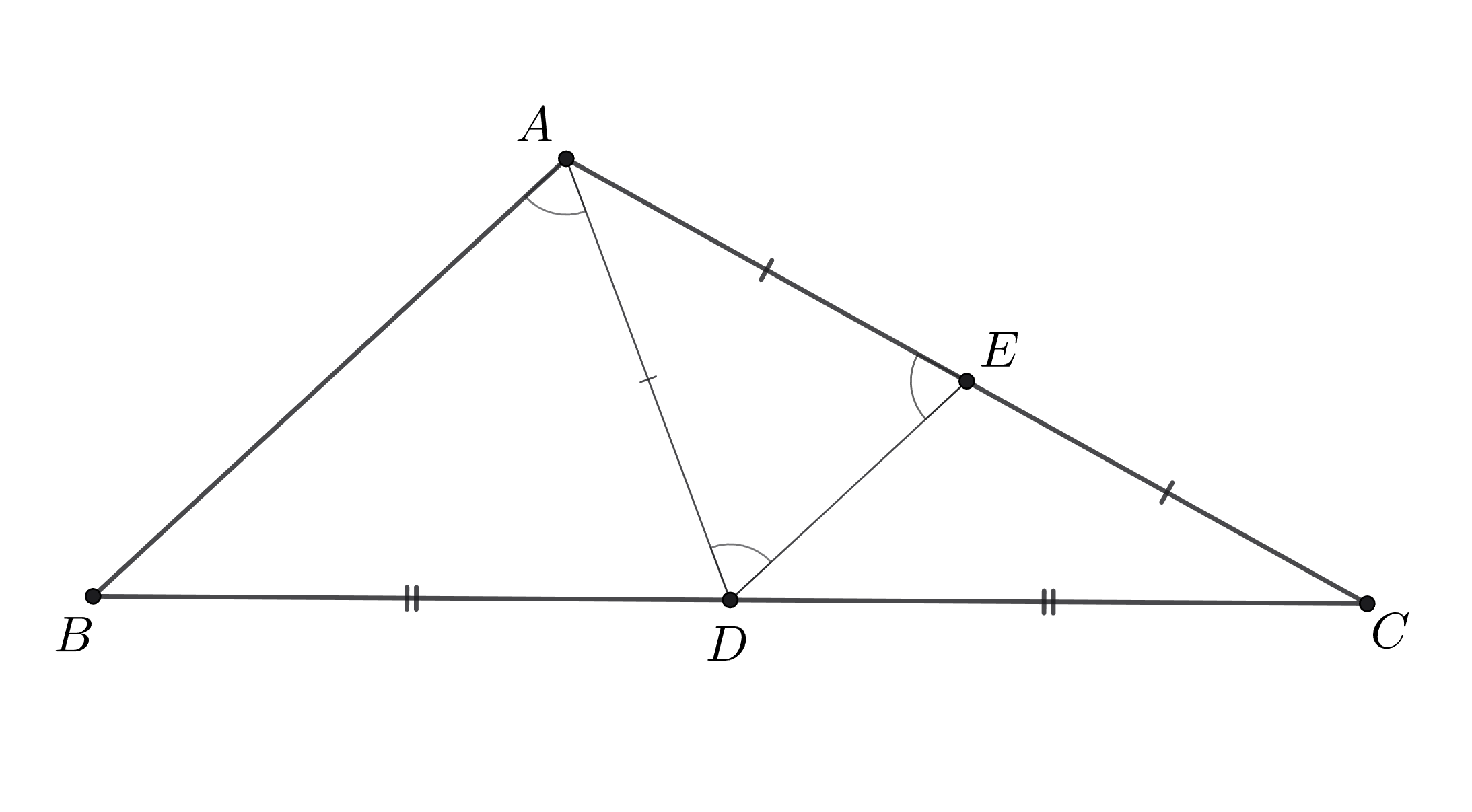
Пусть — середина
. Если
то треугольник
равнобедренный, значит, углы
и
при основании
острые. Осталось заметить, что
т.е. является тупым. Если
то угол
может
быть прямым; если
то угол
может быть прямым.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




