Высоты

Так как , то четырехугольник вписанный. Далее можно рассуждать по-разному.

Первое решение.

По свойству вписанного четырехугольника (см. рис.)

Тогда, используя прямоугольные треугольники и , получим

Аналогично,

Следовательно, .

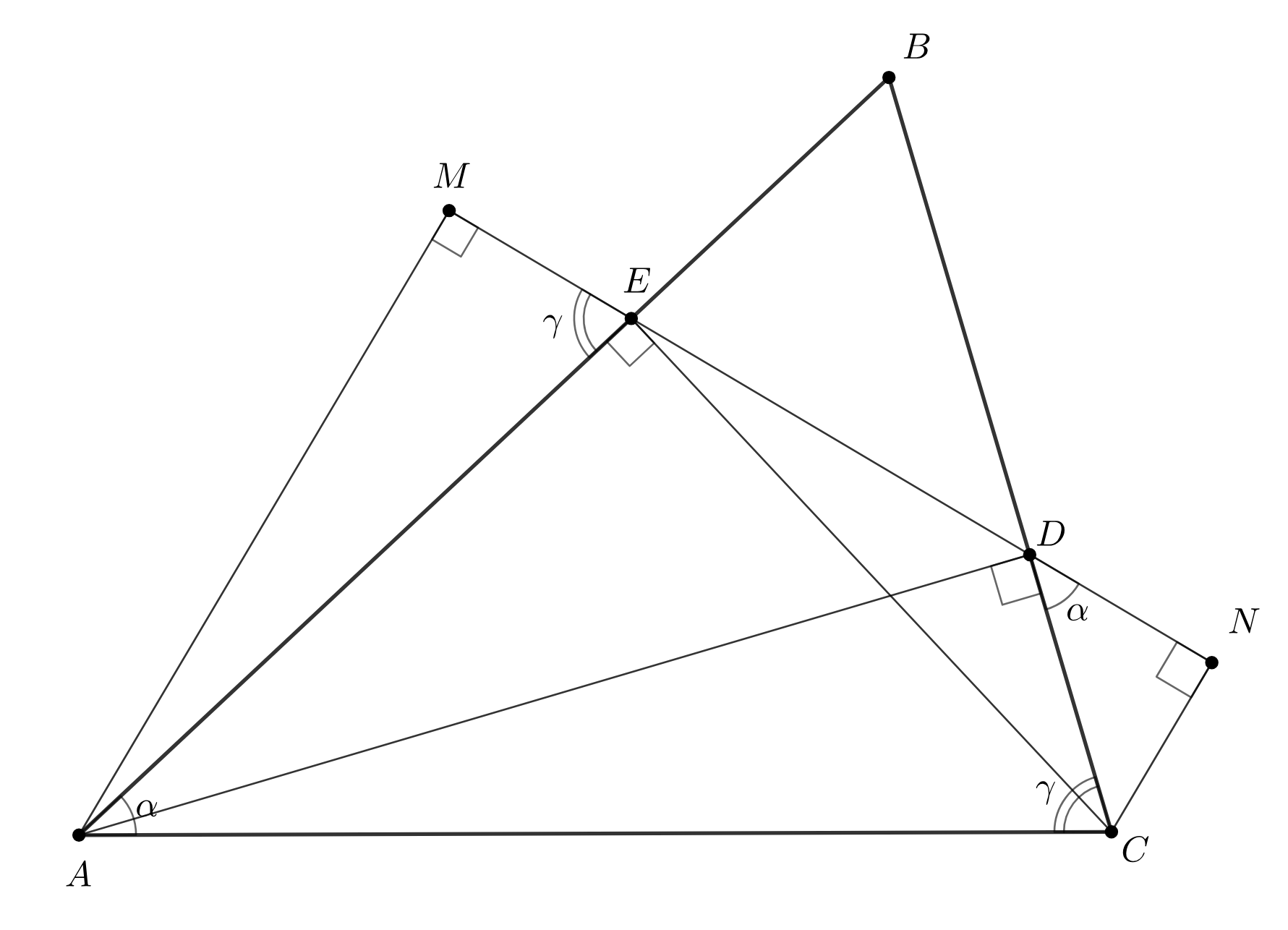
Замечание. Отметим, что использованные равенства углов можно получить из подобия треугольников и , которое, в свою очередь, можно получить из подобия треугольников и (если не использовать окружность).

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Воспользуемся тем, что центром окружности, описанной около , является середина стороны . Так как треугольник равнобедренный, то его высота является и его медианой, те есть (см. рис.). Прямые и перпендикулярны прямой , поэтому параллельны друг другу. Из того, что по теореме Фалеса следует, что . Тогда

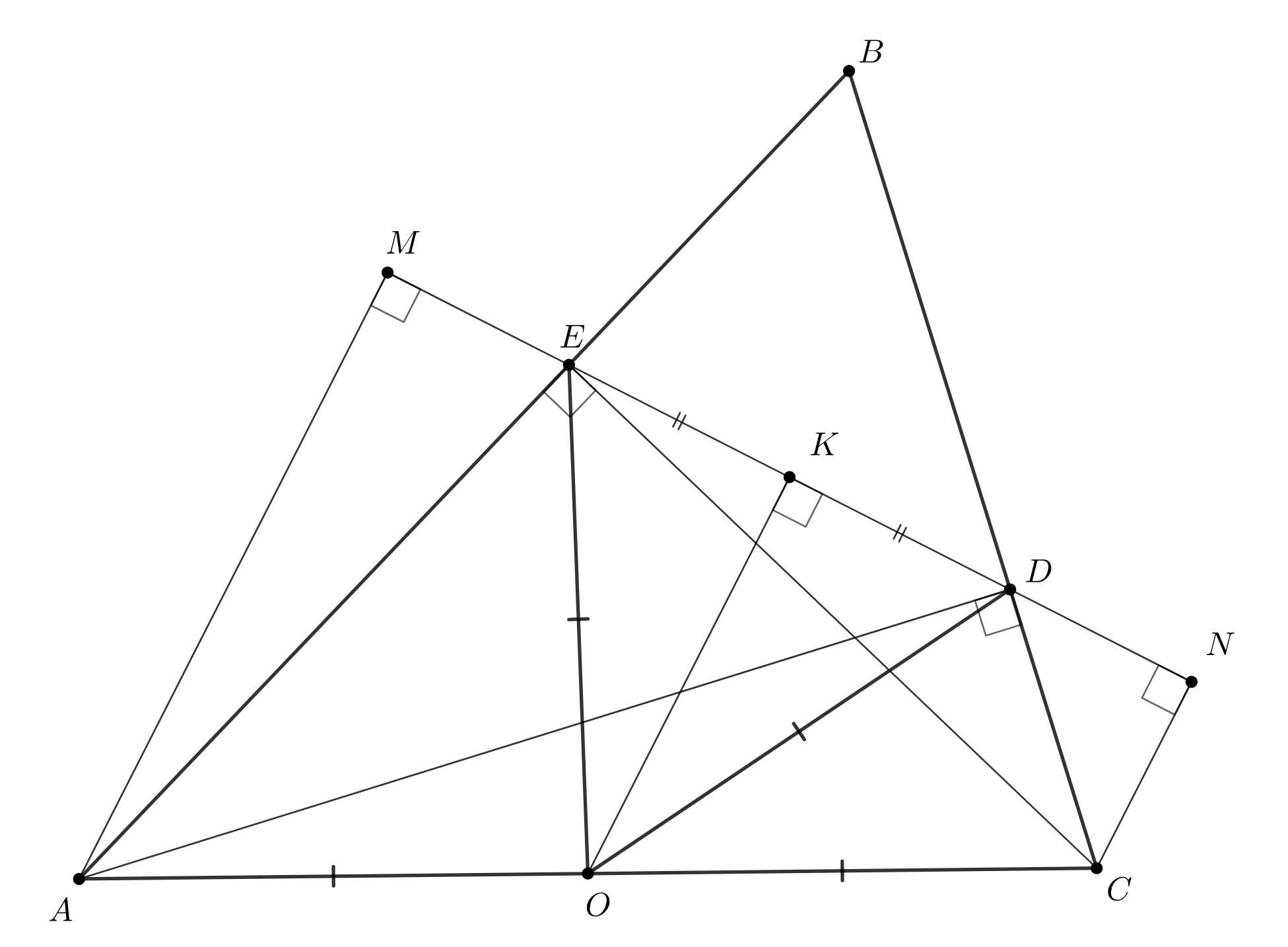
Замечание. В этом способе решения необязательно “напрямую” использовать окружность. Равенство следует из того, что эти отрезки являются медианами прямоугольных треугольников с общей гипотенузой, проведёнными к ней.