Высоты
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике биссектриса острого угла между высотами
и
пересекает стороны
и
в точках
и
соответственно. Докажите, что
Подсказка 1
Попробуем подсчитать углы! Наша цель - доказать равенство углов ∠QPA и ∠AQP . Пусть угол ВАС = α. Тогда попробуйте подсчитать тогда углы АВВ₁ и АСС₁.
Подсказка 2
Далее попробуем подсчитать ∠C₁HP и ∠QHB₁. Они тоже будут равны (не забываем про условие о биссектрисах.) Отсюда уже рукой подать до ∠QPA и ∠AQP!
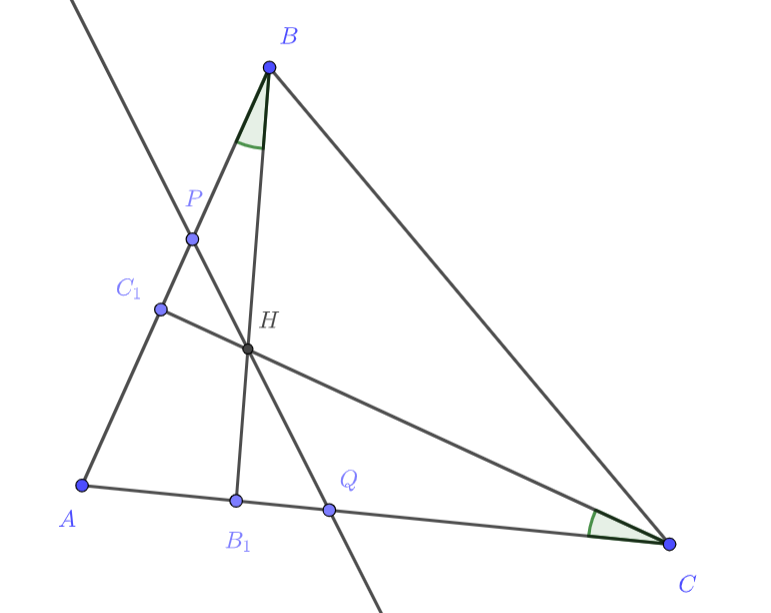
Пусть , откуда
(что также следует из вписанности
). Далее,
, поскольку
— биссектриса. Отсюда сразу же получаем равенство углов
, так что
— равнобедренный, что и требовалось.
Замечание. На самом деле вводить угол было не обязательно, однако полезно для тренировки счёта углов, который пригодится Вам
в других задачах.
что и требовалось доказать
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




