Средняя линия и её свойства

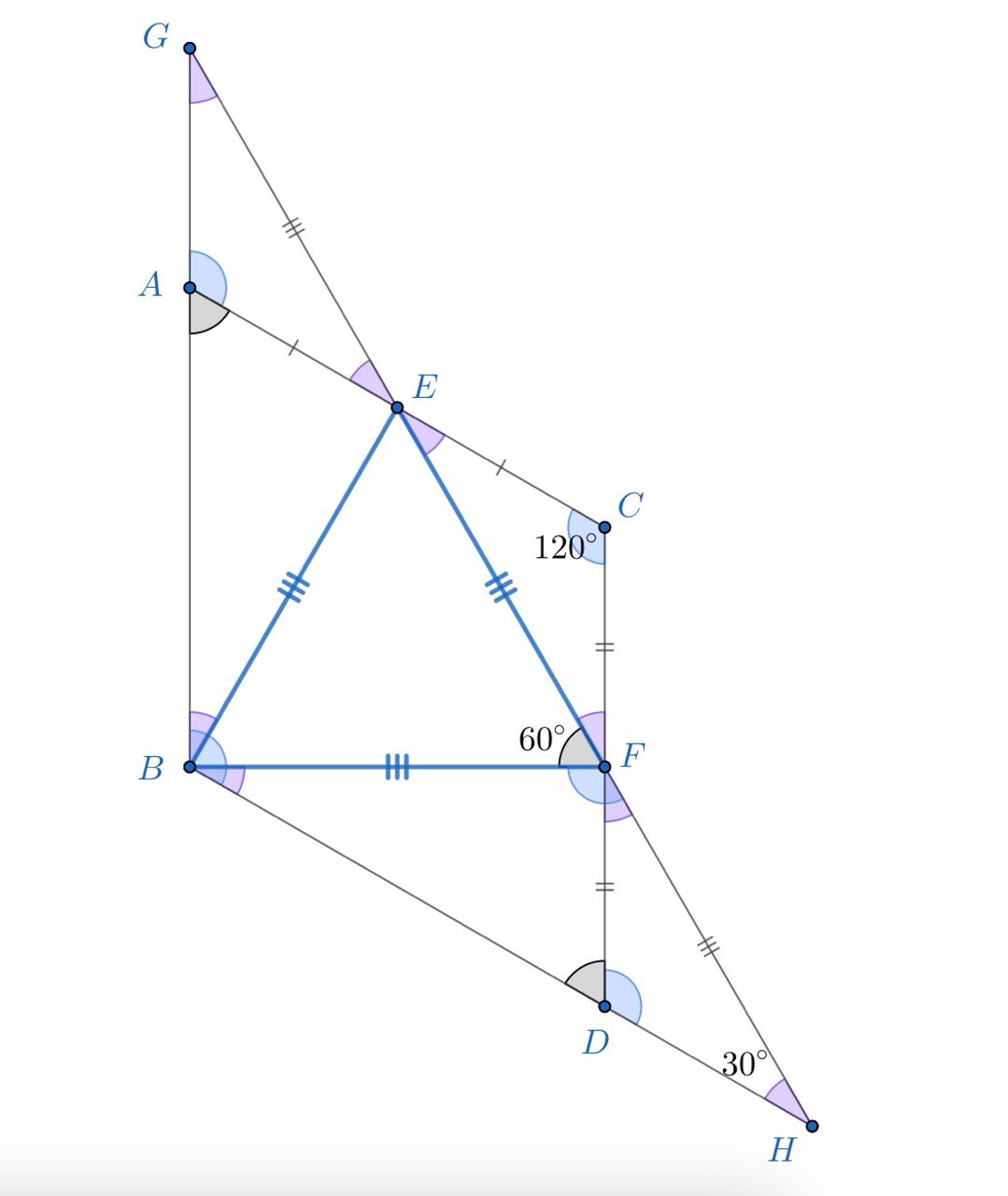
Продлим до пересечения с прямыми и и получим точки и соответственно. Рассмотрим треугольники и . Они равны, почему? , так как — середина отрезка, как вертикальные и как накрест лежащие при параллельных прямых и (ведь нам дан параллелограмм) и секущей . Значит, получается, треугольники и правда равны по стороне и двум прилежащим к ней углам. Аналогично получим, что треугольники и равны по стороне и двум прилежащим к ней углам. А значит, все эти три треугольника равны. Получается, что , но мы ведь знаем, что — равносторонний треугольник, то есть . Значит, треугольник — равнобедренный по определению. Найдем его углы. как смежные, то есть , а углы и равны . То же самое можно сказать про углы и , а значит, . Ну а второй угол в параллелограмме равен .