Параллелограмм
Ошибка.
Попробуйте повторить позже
Вершину параллелограмма соединили с серединой его противоположной стороны. Полученный отрезок образует с другой его стороной угол
. Докажите, что отмеченный на рисунке перпендикуляр равен одной из сторон параллелограмма.
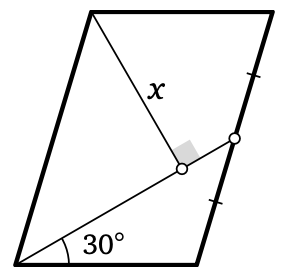
Подсказка 1
В этой задаче будет полезно продлить отрезок, соединяющий вершину с серединой, до пересечения с другой стороной параллелограмма. Угол 30 градусов перекинется как накрест лежащий. Вдруг там возникнет что-то интересное?
Подсказка 2
Не появился ли там прямоугольный треугольник с углом 30 градусов? Что вы про него знаете?
Продлим прямую до пересечения с прямой
Пусть они пересекутся в точке
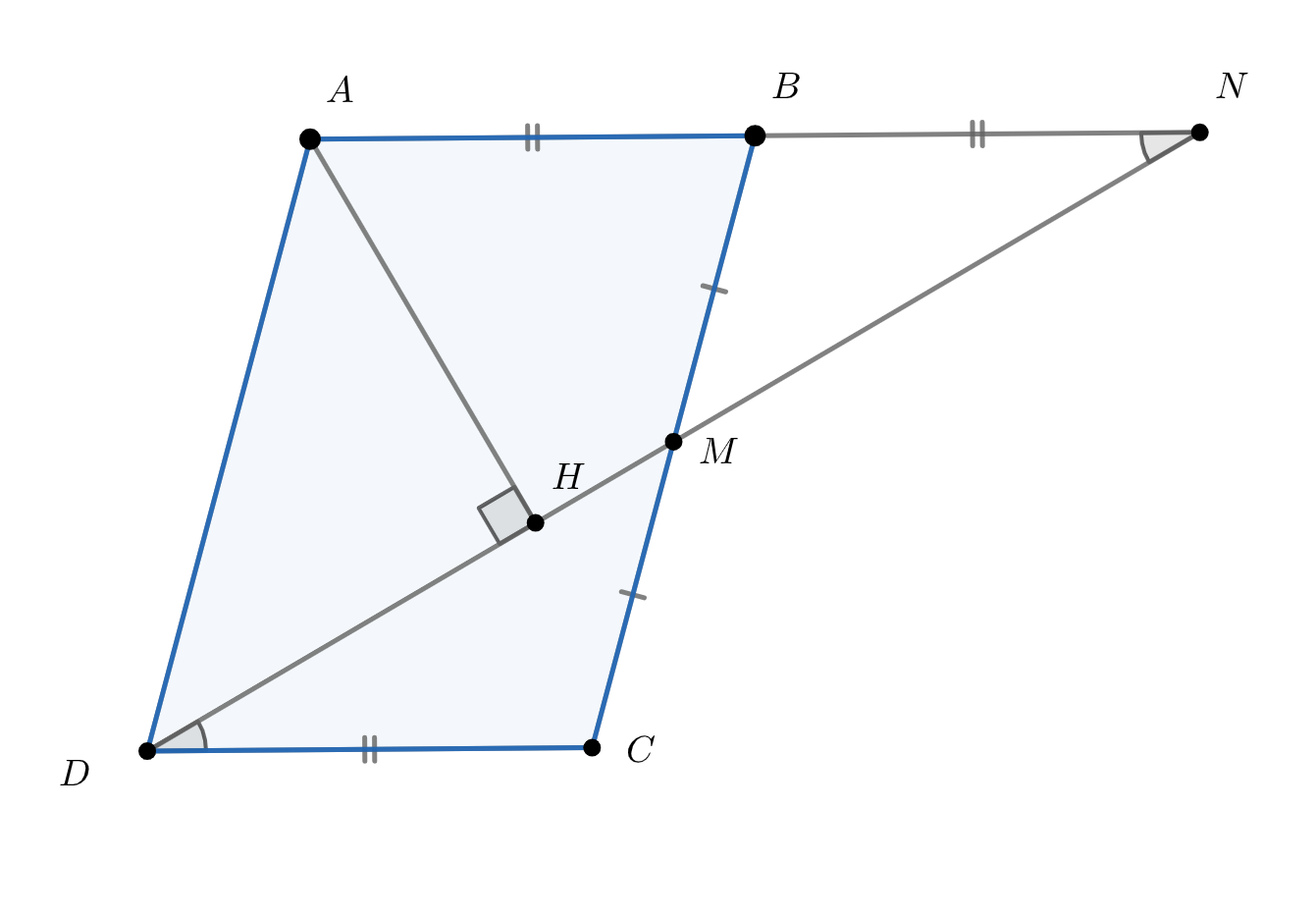
Прямые и
параллельны, так как
— параллелограмм. Отсюда
и
—
накрестлежащие при
и секущих
и
соответственно. Получается,
как
вертикальные,
по условию, то есть треугольники
и
равны по стороне и двум прилежащим к ней
углам. Отсюда следует, что
При этом
по определению параллелограмма, то есть
откуда
Заметим, что треугольник — прямоугольный треугольник с углом
так как
по условию и
По
свойству прямоугольного треугольника с углом
катет, лежащий напротив угла в
в два раза меньше гипотенузы, то есть
Итак, перпендикуляр
равен стороне параллелограмма
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




