Параллелограмм
Ошибка.
Попробуйте повторить позже
Высоты и
параллелограмма
пересекаются в точке
a) Докажите , что прямые и
перпендикулярны;
б) Найдите длину диагонали , если
Замечание. Пункт а) выполнен не во всех случаях.
Источники:
Подсказка 1
Давайте заметим, что в условии не указано, на какие стороны опущены высоты. Значит, возможно несколько вариантов. Рассмотрите их. На всех ли картинках действительно будет выполняться эта перпендикулярность?
Подсказка 2
Давайте во втором пункте сначала рассмотрим случай, когда высоты BE и DK опущены на AD и AB. Мы хотим связать BD с KE и CH. Это совсем нетрудно сделать, если вспомнить про наличие подобных треугольников, связанных с ортоцентром, и теорему синусов.
Подсказка 3:
Давайте обозначим ∠BAD через γ. Треугольники △AEK и △ABD подобны. А знаете, с каким коэффициентом? Теорему синусов же стоит применять где-то в окружности (CBHD), там тоже фигурирует угол γ.
Подсказка 4:
Во втором случае ситуация иная. Можно сразу вычислить sin(γ), если поработать с окружностью (CKHE). Если дальше вспомнить про подобие, то задача решится)
а) Докажем, что в общем случае это неверно. В условии не указаны стороны, на которые опускаются высоты и
а значит,
возможны два варианта: либо точки
и
лежат соответственно на сторонах
и
либо соответственно на сторонах
и
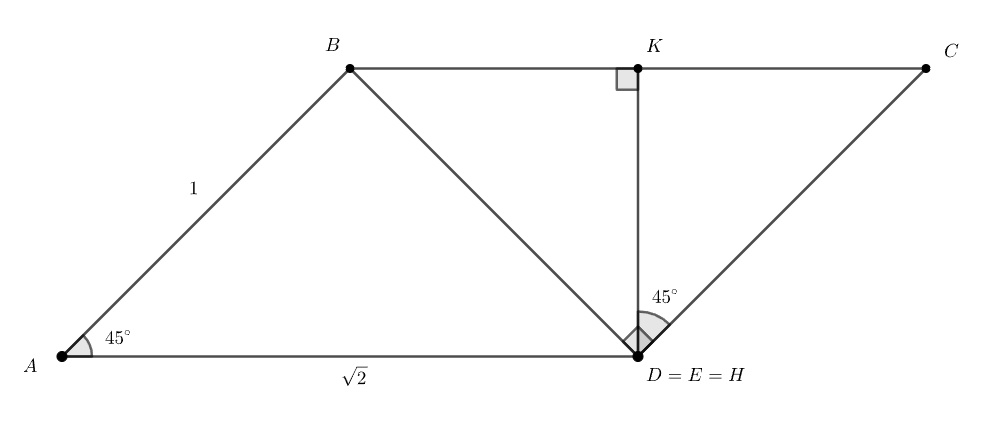
Приведём пример параллелограмма для второго случая, в котором утверждение задачи неверно — пусть
Тогда вершина
совпадает с точками
и
а точка
является серединой
Очевидно, что тогда угол между
и
равен
и они не перпендикулярны.
Замечание. В случае, когда высоты и
опущены на стороны
и
действительно, всегда будет перпендикулярность
между прямыми
и
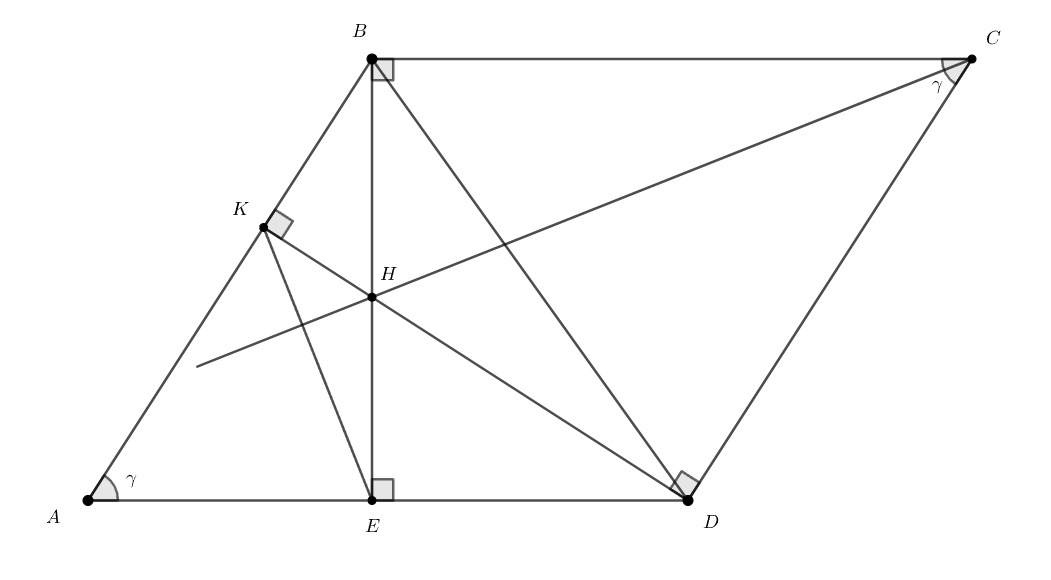
б) Случай Рассмотрим случай, когда высоты
и
опущены на стороны
и
Пусть Треугольники
и
подобны (их углы равны), следовательно,
Для треугольника вписанного в окружность с диаметром
верна теорема синусов:
Подставляя известные значения и
получаем:
Заменяя и подставляя все в выражение тригонометрического тождества, получаем уравнение:
Полученное квадратное уравнение на не имеет решений, так как его дискриминант меньше нуля. Значит, этот случай
невозможен.
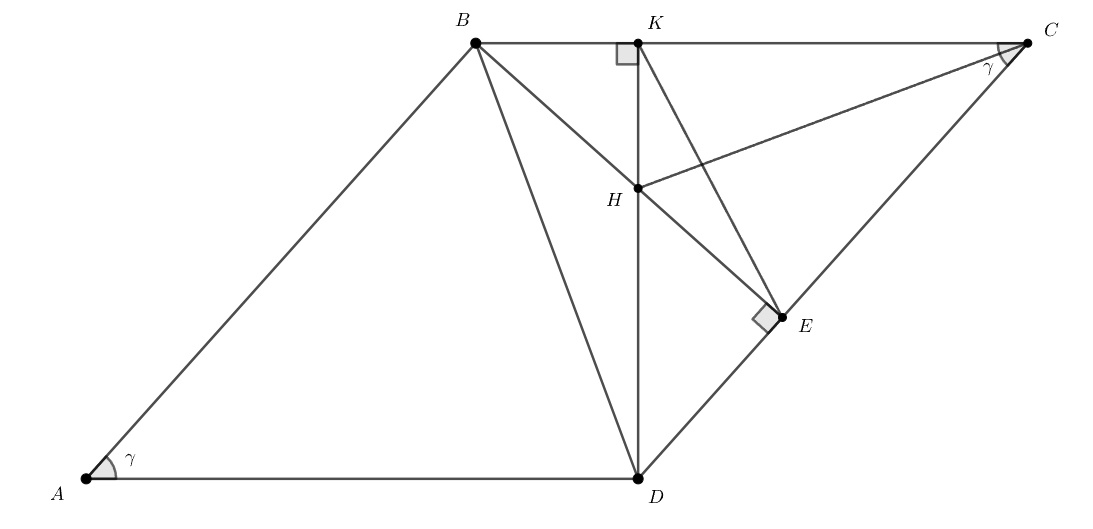
Случай Рассмотрим случай, когда высоты
и
опущены на стороны
и
Для треугольника вписанного в окружность с диаметром
верна теорема синусов:
Таким образом,
Пусть Треугольники
и
подобны (их углы равны), следовательно,
Подставляя находим:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




