Параллелограмм
Ошибка.
Попробуйте повторить позже
На сторонах и
параллелограмма
расположены точки
и
соответственно, причём
Прямые
и
пересекаются в точке
. Найдите отношения
и
Подсказка 1
Сделаем классическое для подобной картинки доп. построение: продлим DN до пересечения с продолжением BC. Назовём Т полученную точку. Пусть ВМ = 2а, тогда МС = 5а. Теперь будем работать с подобиями! Что можно сказать об отношении ВТ к AD? Тогда как выразить ВТ через а?
Подсказка 2
Теперь мы можем выразить ТМ через а и найти отношение ТМ к AD. А как мы можем использовать это отношение для нахождения ОМ:ОА? Может быть найдётся какая-то пара подобных треугольников?
Подсказка 3
Теперь точно так же мы можем найти и ON:OD! Обозначим BN = 2x. Теперь нужно просто продлить АМ до пересечения с продолжением CD (назовём точку пересечения К), найти СК:АВ через подобие, далее выразить DК через х и найти искомое отношение, выделив ещё одну пару подобных треугольников.
Продолжим до пересечения с прямой
в точке
Положим
,
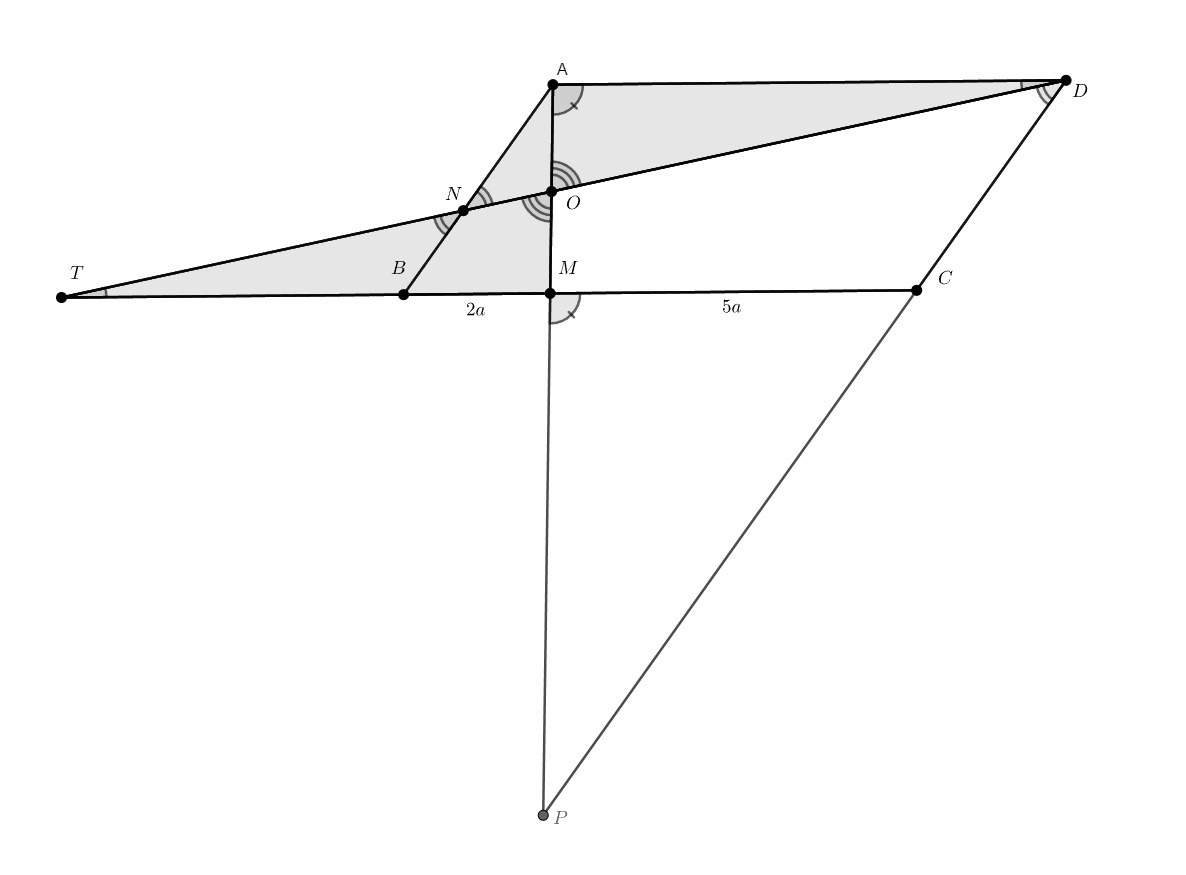
Из подобия треугольников и
(коэффициент
) находим, что
а из подобия треугольников и
— что
Пусть , тогда
, откуда
, поскольку
. Тогда из подобия
и
имеем
;
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




