Параллелограмм
Ошибка.
Попробуйте повторить позже
Середины сторон параллелограмма образуют прямоугольник. Докажите, что данный параллелограмм — ромб.
Подсказка 1
Для начала стоит подумать, как можно доказать, что параллелограмм является ромбом. Какие бывают признаки?
Подсказка 2
Точно! Например, можно попробовать подойти к тому, что диагонали перпендикулярны. Посмотрим повнимательнее на картинку: F и G — середины BC и CD. Значит, FG — средняя линия в треугольнике CBD. А какие хорошие свойства есть у средних линий?
Подсказка 3
Верно! По свойству средних линий FG параллельна BD. А можно ли найти еще пару параллельных отрезков?
Подсказка 4
Конечно! Это отрезки EF и AC по аналогичным причинам. Нас интересует угол между BD и AC. При этом мы знаем, что они параллельны каким-то двум прямым параллелограмма. А что мы знаем об углах между парами параллельных прямых?
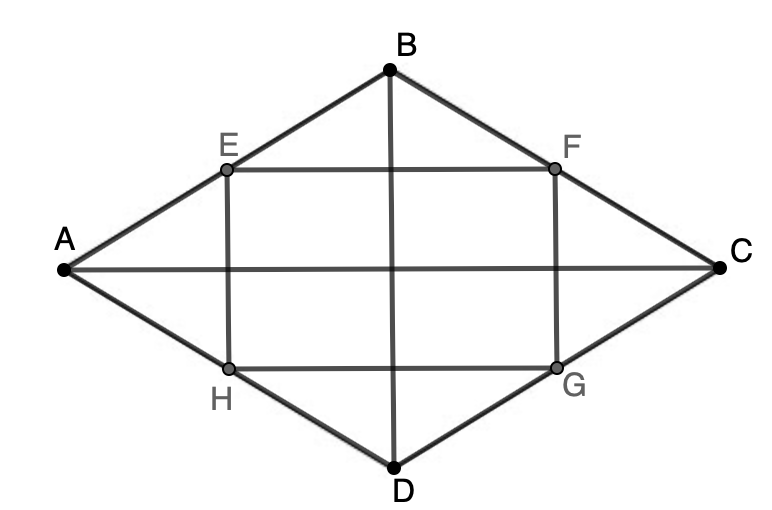
Пусть ,
,
,
— середины сторон данного параллелограмма. Рассмотрим треугольник
. В нем
— средняя линия, так как
делит стороны треугольника пополам, значит,
. Также
— средняя линия в треугольнике
, значит,
.
Так как — прямоугольник,
. Из того, что
, получается, что
перпендикулярна
, а значит, и
, но ведь еще и
, значит,
перпендикулярна
. То есть в параллелограмме диагонали перпендикулярны, а значит, по
признаку он ромб.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




