Параллелограмм
Ошибка.
Попробуйте повторить позже
На каждой из сторон параллелограмма выбрано по произвольной точке. Точки на соседних сторонах параллелограмма соединены отрезками прямых. В результате от параллелограмма оказываются отсеченными четыре треугольника. Вокруг каждого из этих треугольников описана окружность. Докажите, что центры этих окружностей являются вершинами некоторого параллелограмма.
Источники:
Подсказка 1
Взглянув на условие, кажется, что надо доказать что-то страшное и непонятно, как это делать. Но давайте вспомним, какие в принципе у нас есть способы решения задач по планиметрии? Углы считать мы не пойдём, в лоб доказывать равенство сторон тоже. Как можно сделать это хитрее?
Подсказка 2
Верно, давайте попробуем воспользоваться векторами. Пусть O_1O_2O_3O_4 наш предполагаемый параллелограмм. Если мы направим попарно в одном направлении вектора O_1O_2, O_3O_4 и O_2O_3, O_1O_4, то нам нужно будет только доказать равенство отрезков. Учитывая, что мы рассматриваем центры окружностей, лежащих на серединных перпендикулярах, что можно сказать про проекции векторов на стороны параллелограмма?
Подсказка 3
Да, проекции будут равны половине стороны исходного параллелограмма. Но тогда получаем, что наши вектора равны, если введём две оси, параллельные сторонам параллелограмма. Победа!
Изобразим окружности и их центры, которые обозначим Рассмотрим векторы
и
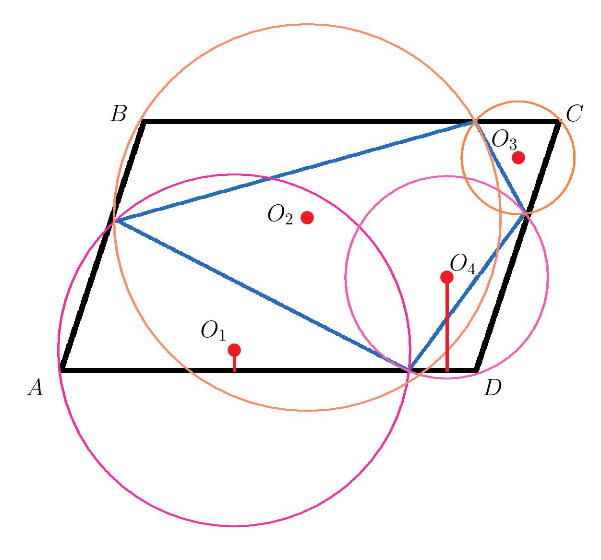
Поскольку центры описанных окружностей лежат на пересечении серединных перпендикуляров, проекции указанных векторов на стороны исходного параллелограмма будут равны половине этих сторон.
Таким образом, если ввести две оси: одну параллельно стороне а другую параллельно стороне
то каждая пара
рассматриваемых векторов будет иметь одинаковые проекции на каждую из введенных осей. Отсюда следует попарное равенство самих
векторов.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




