Прямоугольники
Ошибка.
Попробуйте повторить позже
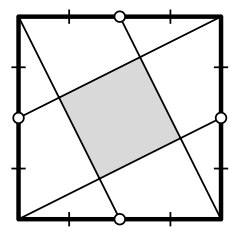
Вершины квадрата соединили отрезками с серединами сторон так, как показано на рисунке. Докажите, что закрашенная на рисунке фигура — квадрат.
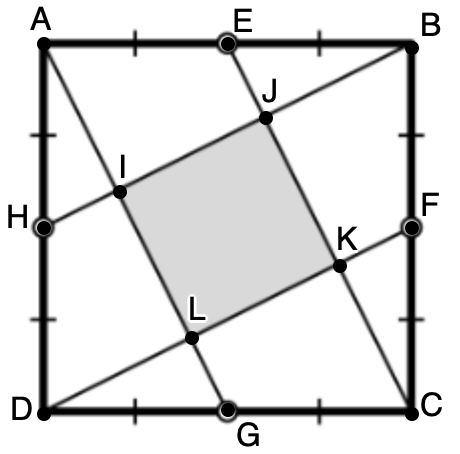
Рассмотрим треугольники 
и 
. В них: 
как стороны квадрата, 
как половины сторон квадрата и
. Значит, по двум сторонам и углу между ними эти треугольники равны. Аналогично можно получить, что
треугольники 
, 
, 
и 
равны. Отсюда: 
и 
как соответственные в равных треугольниках. Теперь рассмотрим треугольники 
, 
, 
, 
. Они будут равны по стороне
и двум прилежащим к ней углам, так как 
и все соответственные углы равны по выше доказанному. И значит, углы
, 
, 
, 
равны как соответственные в равных треугольниках, и углы 
, 
, 
, 
равны как
вертикальные с равными.
Также из равенства треугольников 
, 
, 
и 
мы узнаем, что 
, а из равенства
треугольников 
, 
, 
, 
– что 
и 
. Тогда что можно сказать про
отрезки 
, 
, 
, 
? Каждый из них равен 
, то есть они все равны.
Итог: в четырехугольнике 
все стороны и все углы равны, значит, он квадрат.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
