Прямоугольники
Ошибка.
Попробуйте повторить позже
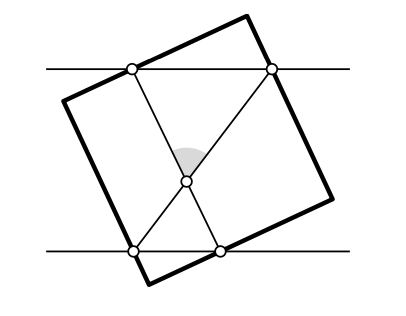
Две прямые, расстояние между которыми равно стороне квадрата, пересекают его стороны в четырех точках так, как это показано на рисунке. Найдите угол между двумя отмеченными отрезками, соединяющими эти точки.
Подсказка 1
Начнём с важной леммы. Если имеется две полосы одинаковой ширины, то их пересечением будет ромб. Докажите эту лемму, прежде чем применять.
Подсказка 2
Ещё один интересный факт. Угол между двумя прямыми равен углу между перпендикулярными им прямыми. Это тоже обязательно докажите!
Подсказка 3
Теперь подумаем, как эти два факта использовать для решения задачи. Нужно бы найти прямые, перпендикулярные отмеченным отрезкам. А в ромбе диагонали перпендикулярны. Точно, нужно найти пары полос, которые образуют ромбы, среди диагоналей которых есть отмеченные отрезки!
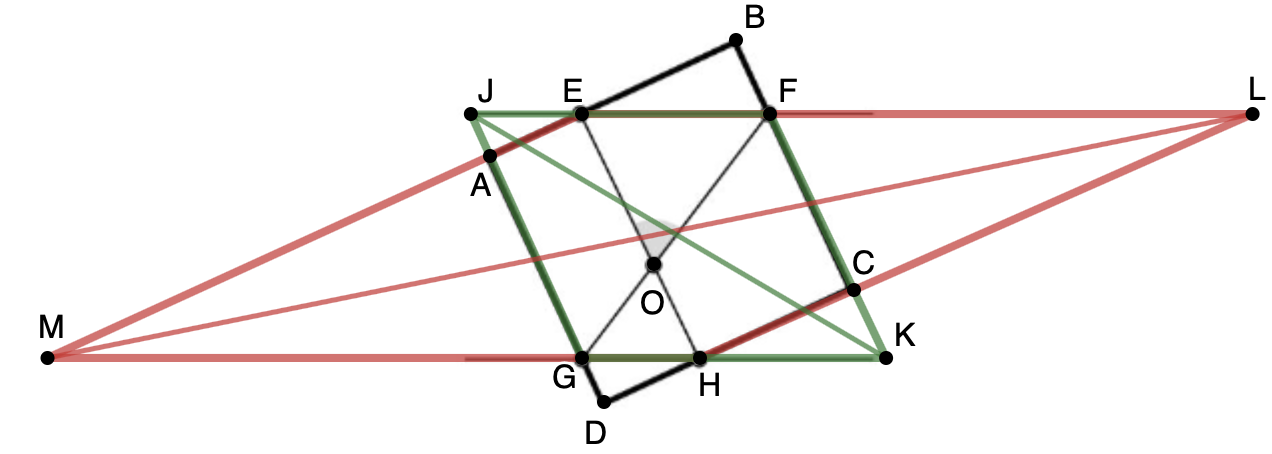
Продлим некоторые отрезки так, как показано на рисунке и вспомним вторую задачу из этой домашки. Рассмотрим полосы, образованные
прямыми и
и прямыми
и
. Что можно сказать про ширину каждой из них? Они обе равны стороне квадрата. Значит,
эти полосы образуют ромб
. Аналогично полосы, образованные прямыми
и
и прямыми
и
, образуют ромб
.
Нам нужно найти угол между прямыми и
. Для этого можно найти угол между перпендикулярами к этим прямым. Почему
так? Давайте докажем.
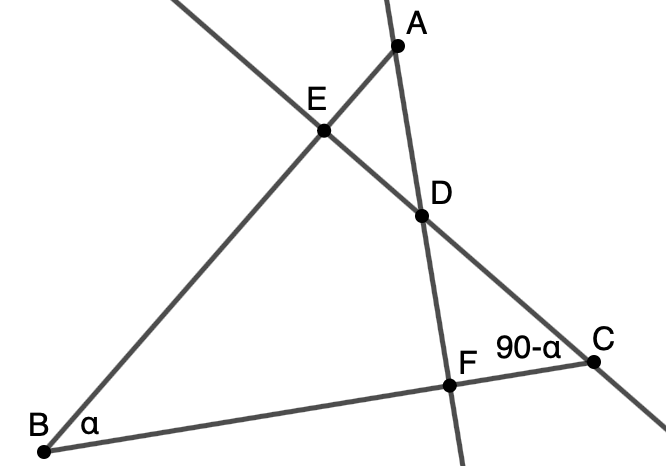
Пусть дан .
,
— перпендикуляры, опущенные на стороны этого угла. Тогда
.
Значит,
.
Понятно, что ,
— диагонали ромбов
и
соответственно. Тогда проведем вторые диагонали этих ромбов. Они
будут перпендикулярным первым, а значит, достаточно будет найти угол между ними, то есть сейчас будем искать угол между прямыми
и
.
Пусть , а
, при этом
, так как
как угол квадрата.
как вертикальный
к
.
как угол, смежный углу квадрата. Тогда
. Аналогично посчитав, получим, что
.
Угол между и
равен
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




