Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
Высоты остроугольного треугольника
пересекаются в точке
Биссектриса угла
пересекает отрезок
в
точке
биссектриса угла
пересекает отрезок
в точке
Обозначим величину угла
через
Аналогично определим
и
Найдите значение суммы
Источники:
Подсказка 1
Идея решения такая. Каждый из этих трёх углов — сумма углов, которые образуют его стороны с высотой. Давайте разобьём эти уголки на пары, чтобы в каждой сумма углов была 90°.
Подсказка 2
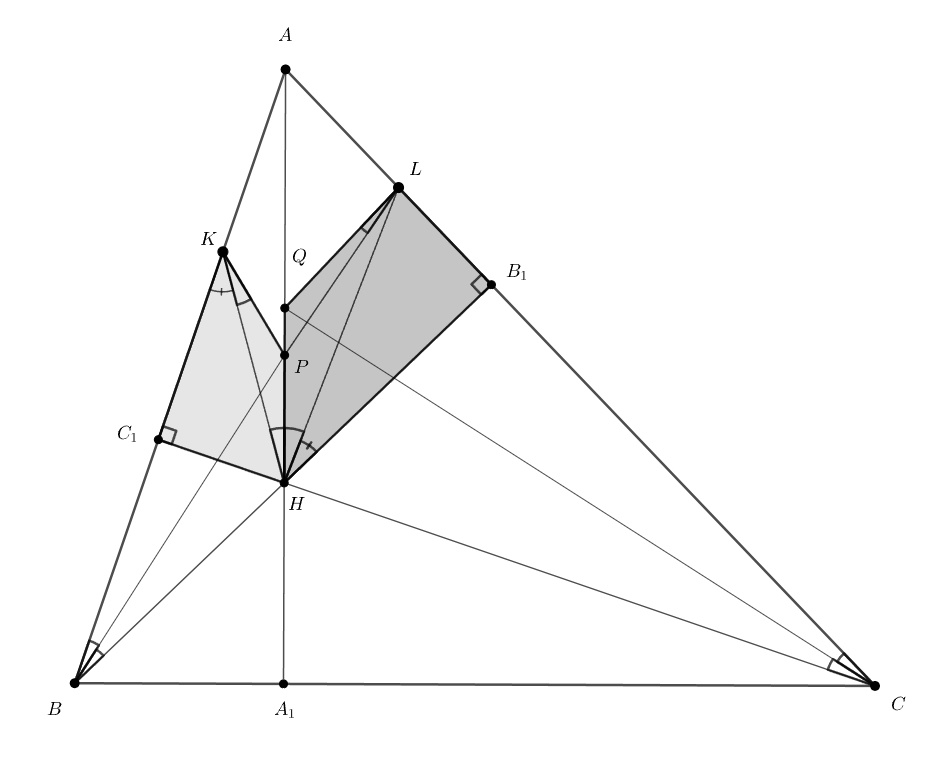
Пусть биссектрисы углов ABH и BCH пересекают AH в P и Q. Докажите, что углы PC₁H и AB₁Q равны. Для остальных пар будет аналогично.
Подсказка 3
Пусть K и L — точки пересечения описанных треугольников BHP И CHQ с AB и AC. Попробуйте доказать, что четырёхугольники KBHP и LCHQ подобны. Тогда диагонали C₁P и QB₁ буду образовывать равные углы со сторонами AB и AC.
Подсказка 4
Чтобы доказать из подобие, докажите подобие их элементов -—треугольников KPH и HQL, а также KC₁H и HB₁L.
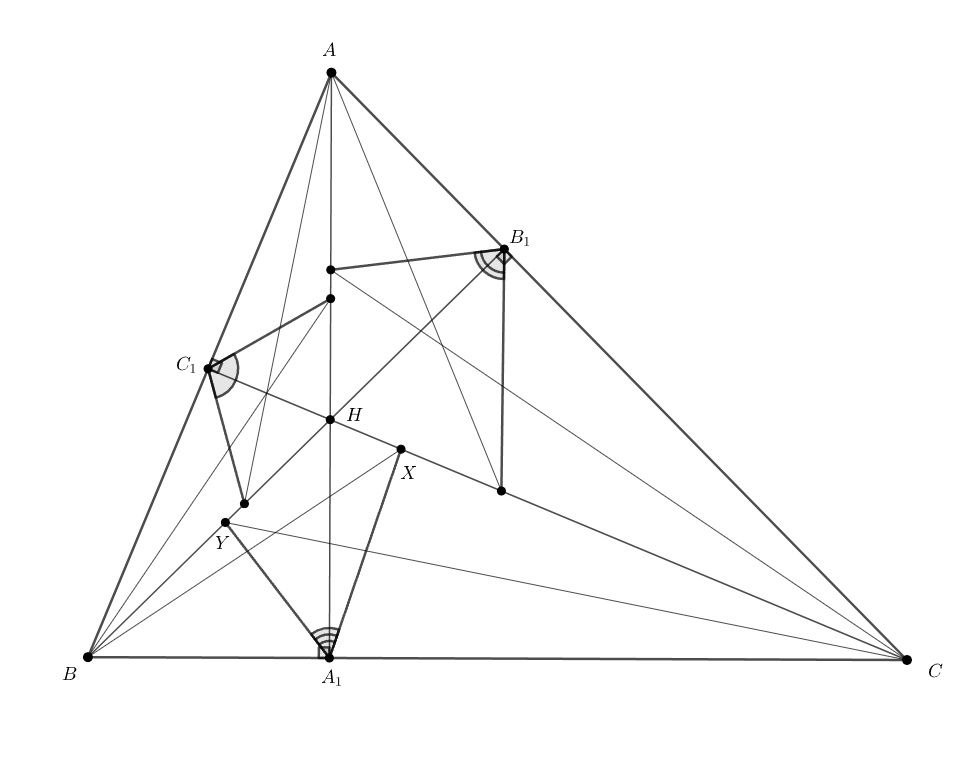
Обозначим точки пересечения биссектрис углов и
с отрезком
через
и
соответственно. Докажем,
что
Из этого будет следовать решение задачи — сумма из условия разбивается на три пары углов с суммой , то есть искомая сумма будет
равна
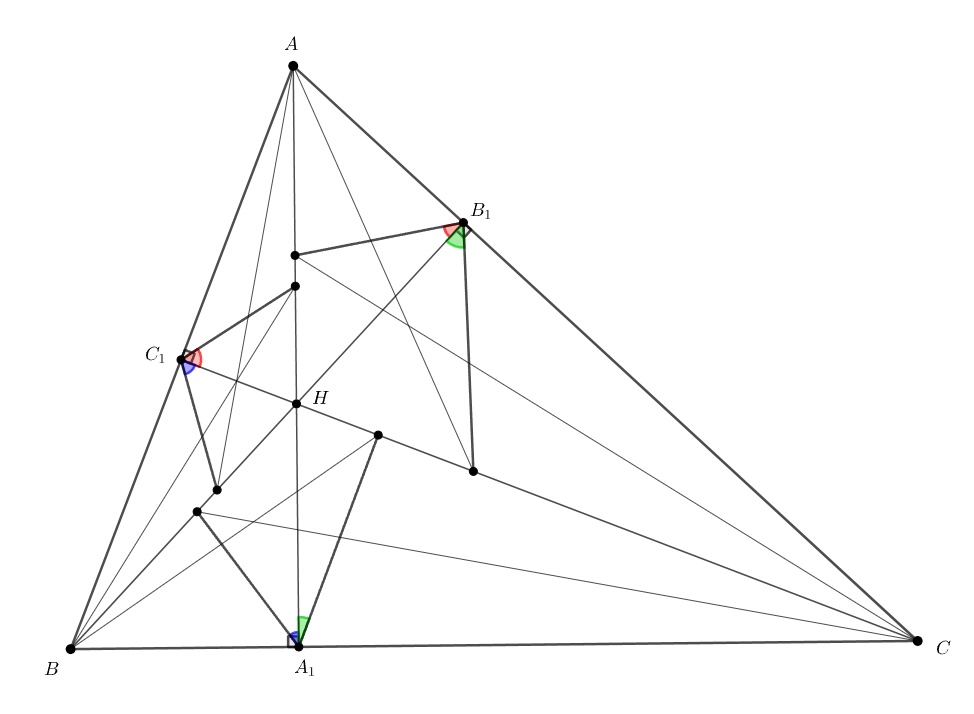
Первый способ. Так как то и
поэтому
Следовательно, прямоугольные треугольники и
подобны по двум углам, поэтому
Как известно, треугольники и
подобны треугольнику
а, следовательно, подобны друг другу.
Отсюда
Из равенств (1) и (2) следует, что
Как известно, поэтому треугольники
и
подобны по углу и отношению прилежащих сторон,
откуда
Тогда
что и требовалось доказать.
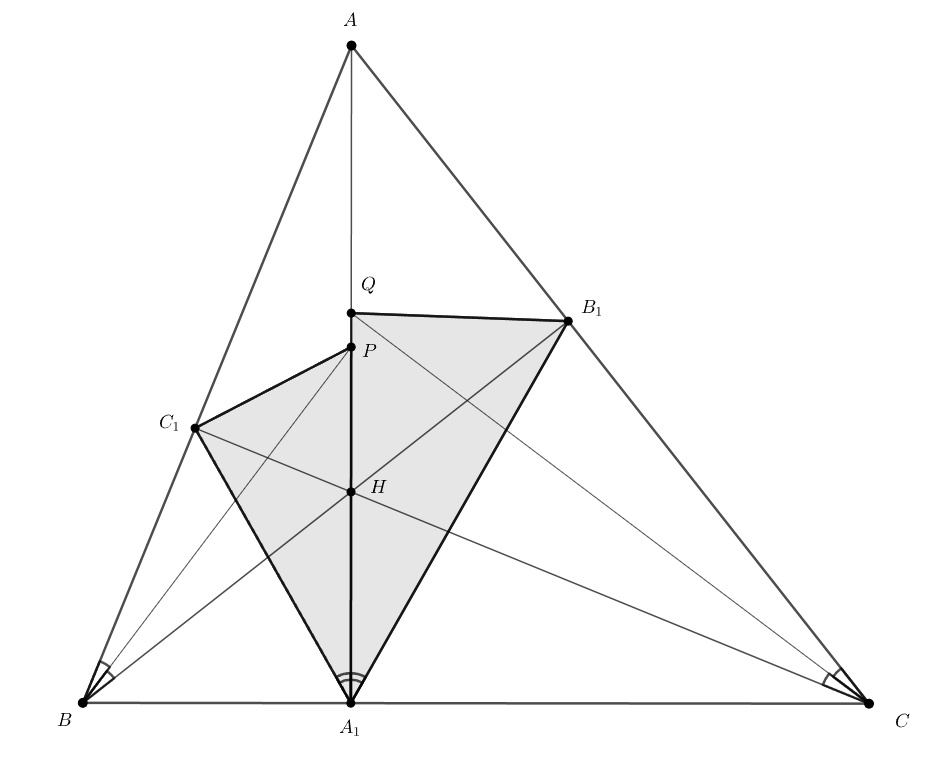
_________________________________________________________________________________________________________________________________________________________________________________
Второй способ. Пусть — точка, изогонально сопряжённая
относительно треугольника
Так как
то точки и
— соответствующие точки в подобных треугольниках
и
Тогда
что и
требовалось доказать.
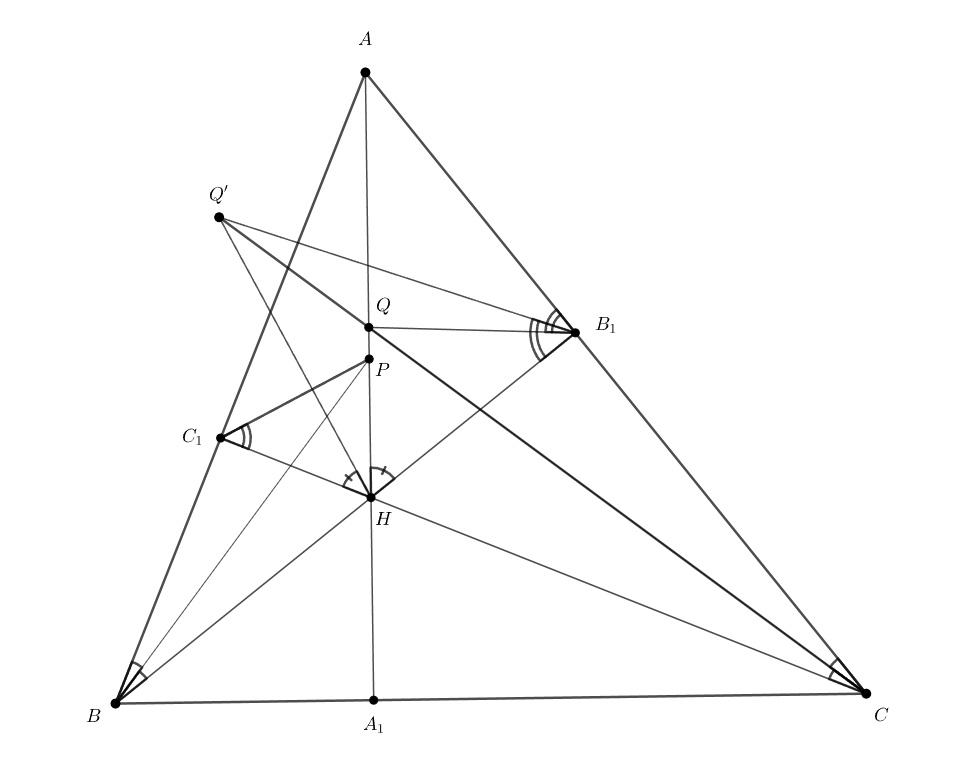
_________________________________________________________________________________________________________________________________________________________________________________
Третий способ. Пусть и
— точки пересечения описанных окружностей треугольников
и
с прямыми
и
соответственно. Так как четырёхугольник
вписанный, то
Так как четырёхугольник вписанный, то
Таким образом, треугольники и
подобны по двум углам. Поскольку четырёхугольник
вписанный, то
поэтому
Таким образом, прямоугольные треугольники и
подобны по двум углам. На гипотенузах
и
подобных треугольников
и
построены соответствующим образом подобные треугольники
и
Следовательно, полученные четырёхугольники
и
подобны. Тогда диагонали
и
образуют
одинаковые углы с соответствующими сторонами
и
то есть
что и требовалось доказать.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




