Вписанные углы и счёт углов в окружности

Поскольку четырёхугольники вписанные, то

Так как

то точки и лежат по разные стороны от прямой В частности, мы показали, что точка лежит строго внутри треугольника

Тогда

поэтому четырёхугольник также является вписанным.

Далее можно рассуждать по-разному.

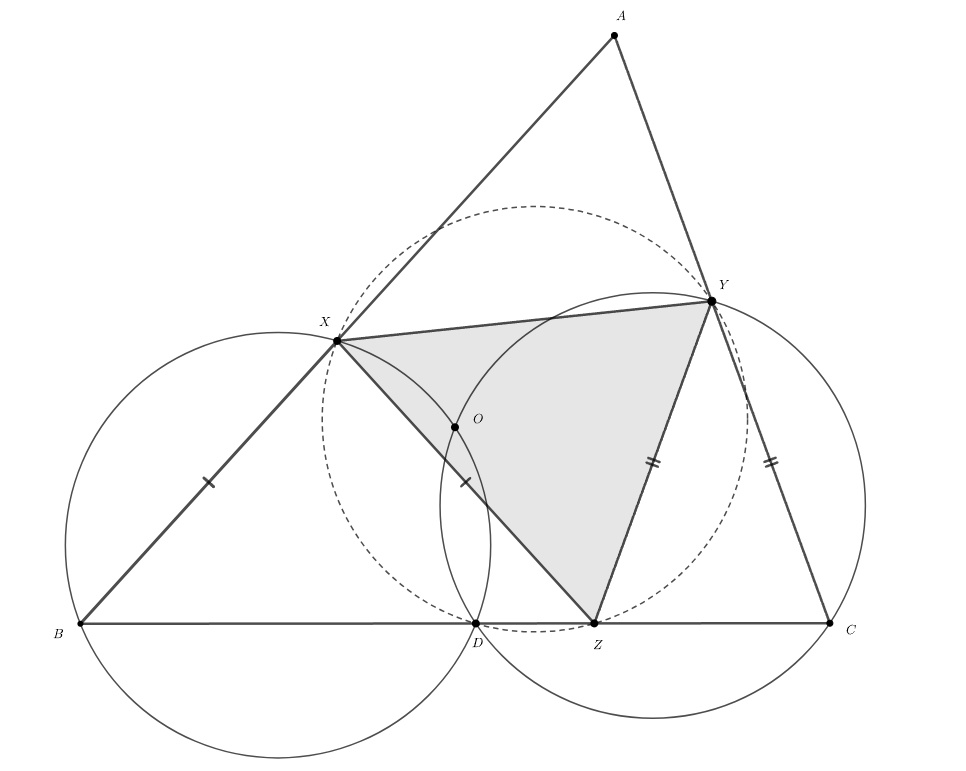
Первый способ. Пусть точка отличная от на отрезке такова, что Тогда поскольку треугольник равнобедренный, Заметим, что

Значит, откуда следует (вне зависимости от порядка расположения точек и на отрезке ), что точки и лежат на одной окружности. Следовательно,

Поэтому треугольник равнобедренный и Получаем, что треугольник составлен из отрезков и равных и соответственно, что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Второй способ. Пусть точки симметричны точкам и относительно середин и сторон и соответственно

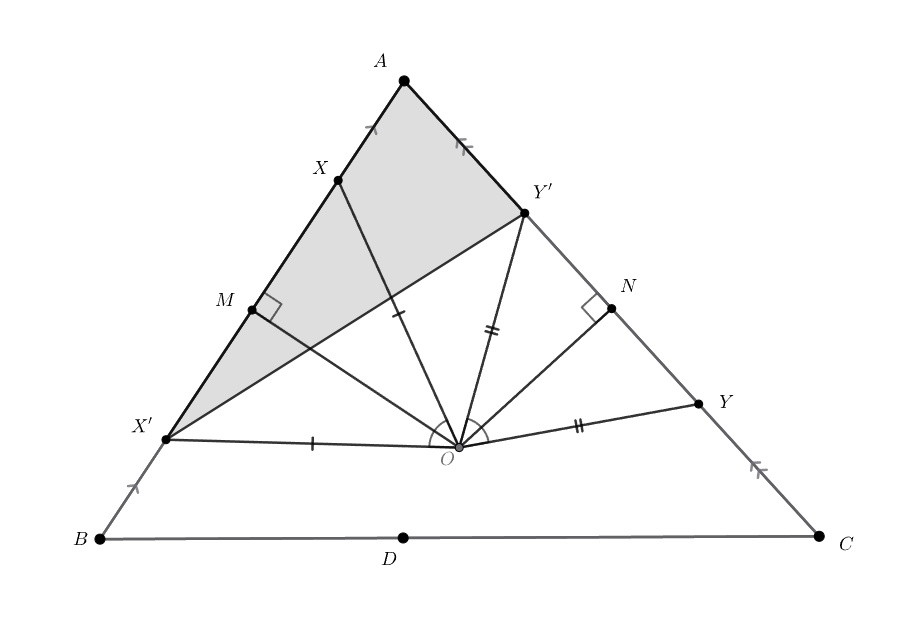
Поскольку — точка пересечения серединных перпендикуляров к сторонам треугольника, Тогда из четырёхугольников находим

Не ограничивая общности, предположим, что лежит на отрезке Поскольку точка лежит на отрезке Получаем, что

Следовательно, треугольники и равны по двум сторонам и углу между ними (на самом деле, мы показали, что они совмещаются поворотом с центром в точке на угол Тогда Поскольку из симметрии, получаем, что треугольник составлен из отрезков, равных и что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Третий способ. По теореме синусов радиус окружности, описанной около равен а радиус окружности, описанной около равен Поскольку получаем, что радиусы этих двух окружностей равны. Проводя аналогичное рассуждение для четырёхугольников и получаем, что радиусы окружностей, описанных около всех трёх четырёхугольников и равны. Обозначим эти окружности соответственно

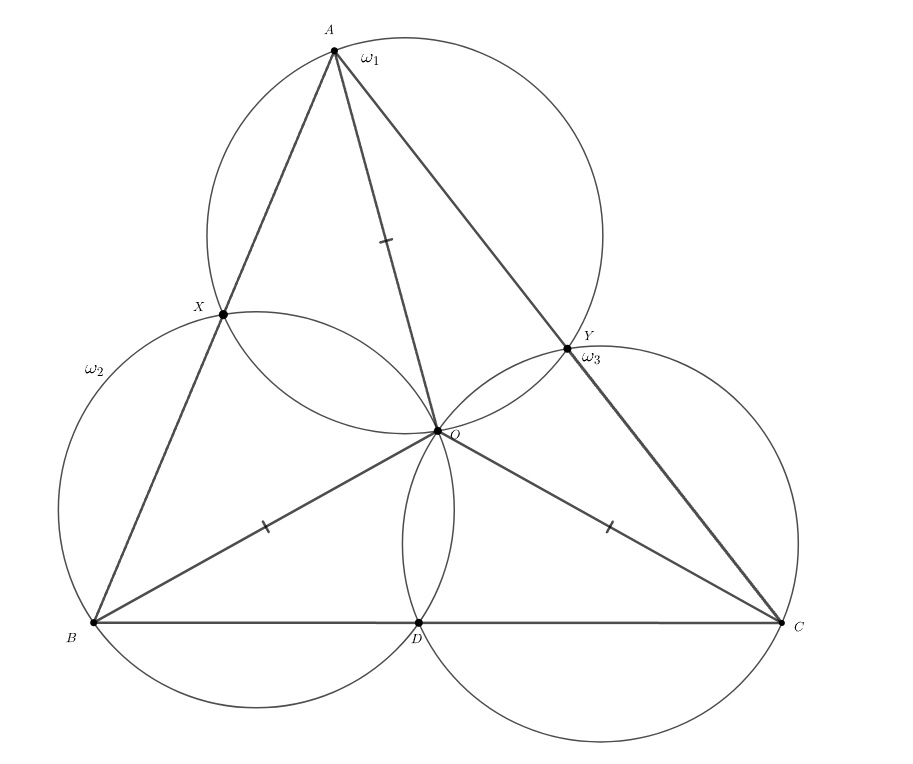
Для того чтобы показать, что из отрезков можно сложить треугольник, достаточно проверить, что вписанные углы, опирающиеся на эти отрезки в окружностях соответственно, в сумме дают

Убедимся в этом. Заметим, что

Таким образом,

что и требовалось доказать.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Отметим, что во всех трёх способах решения неявно предполагается, что точки и отличны от Тем не менее все три рассуждения можно уточнить и в противном случае. Например, если точка совпадёт с точкой то утверждение о вписанности четырёхугольника из решения нужно заменить на утверждение о касании описанной окружности треугольника стороны в точке