Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
Высоты и
остроугольного неравнобедренного треугольника
пересекаются в точке
Точка
— середина стороны
Описанная окружность треугольника
пересекает отрезок
в точке
Докажите, что
— биссектриса угла
Источники:
Подсказка 1
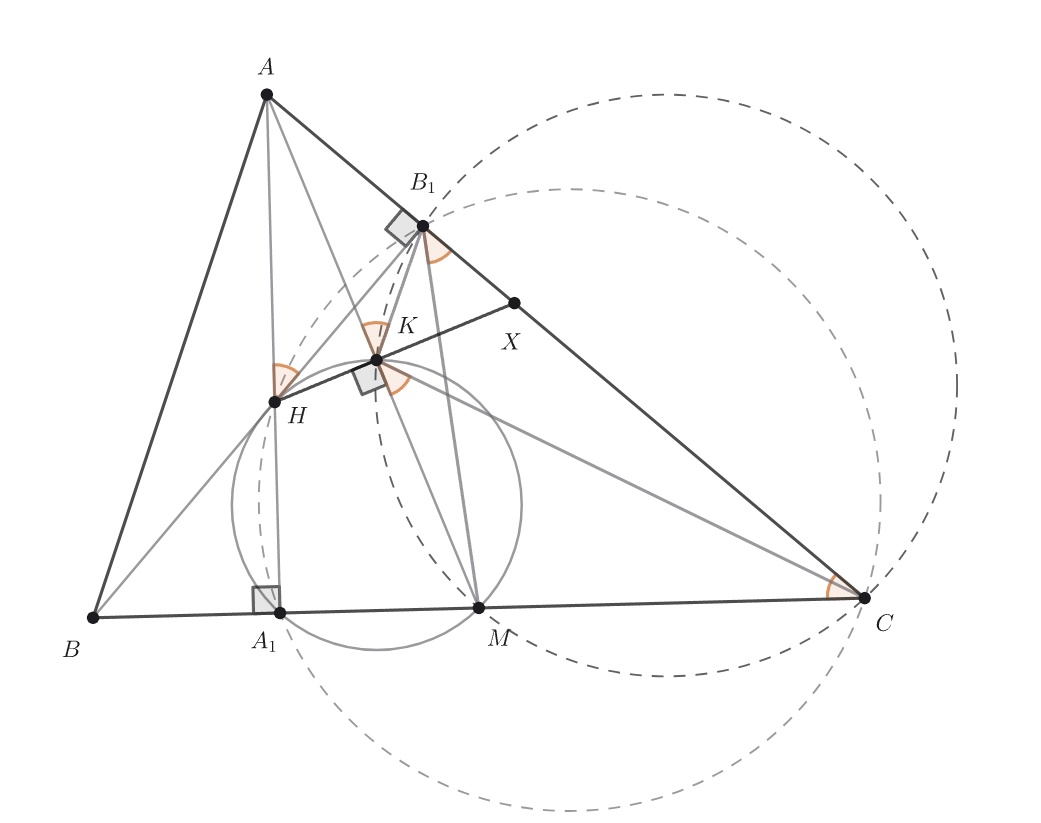
Если в контексте задачи фигурирует ортоцентр, то на картинке скорее всего будет много вписанных четырёхугольников и эта задача — не исключение.
Подсказка 2:
Обратите внимание на четырёхугольники MKB₁C и A₁HB₁C, а также на степень точки A относительно соответствующих окружностей и найдите ещё вписанные четырёхугольники.
Подсказка 3:
Если вы всё сделали верно, то четырёхугольники MKB₁C, A₁HB₁C, A₁HKM, AHKB₁ должны быть вписанными. Для завершения решения поперекидывайте угол ACB в окружностях.
Так как — высота, то
Аналогично
Тогда
— вписанный четырёхугольник, так как
Степень точки
относительно окружности
с одной стороны равна
с другой —
То есть
тогда
— вписанный, и аналогично из степени точки
получаем, что
Итого,
то есть — вписанный.
Так как и
— смежные углы и
— вписанный, то
откуда
Так как
— вписанный, то
из-за того, что и
— смежные углы. А также получаем:
Отсюда — вписанный, тогда
Из вписанности знаем, что
а из смежности знаем, что
Тогда
В треугольнике
и точка
— середина гипотенузы, значит,
то есть треугольник
—
равнобедренный, тогда:
Так как — вписанный, то
Тогда получаем, что:
— вписанный, тогда
так как
То есть
значит,
где
Получаем:
то есть значит,
— биссектриса
Что и требовалось доказать.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




