Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведена высота
и отмечена точка пересечения высот
Серединный перпендикуляр к
отрезку
пересекает окружность, описанную около треугольника
в точках
и
Докажите, что
Источники:
Заметим, что так что
— средняя линия прямоугольного треугольника
Значит,
пересекает гипотенузу
в
её середине
так что
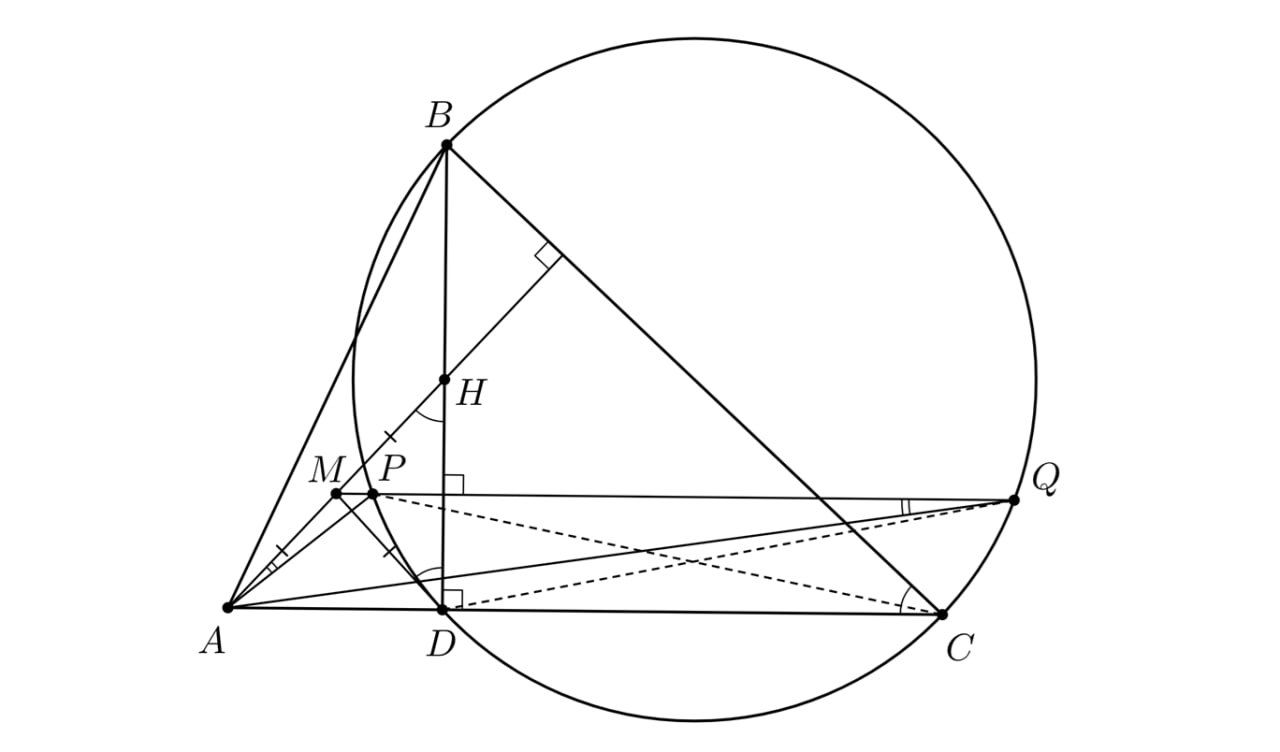
Имеем а поскольку
и
имеем также
Получаем равенство
из которого следует касание прямой
и окружности
в точке
Отсюда
(по теореме о
произведении отрезков секущей).
Далее, Значит, треугольники
и
подобны (угол
общий и
). Отсюда
поэтому
Итак, и, поскольку
для завершения решения остаётся убедиться, что
Для определённости далее считаем, что лежит между
и
Имеем
Так как то дуги
и
равны, а значит, опирающиеся на них вписанные углы равны. Тогда
что завершает доказательство.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




