Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
Пусть — отражение вершины
остроугольного треугольника
относительно
Отрезки
пересекают описанную
окружность треугольника
в точках
и
Докажите, что
— биссектриса угла
Подсказка 1
Если мы планируем решать задачу через счёт углов, то было бы неплохо зафиксировать картинку, чтобы точно знать, что всё посчитается. Как это сделать? Хватит двух углов треугольника ABC, при этом нужно взять два удобных. Давайте углы B и C обозначим неизвестными, после чего попробовать выразить все остальные углы!
Подсказка 2
Чтобы доказать равенство углов (то есть, доказать, что AD — биссектриса), нужно доказать равенство соответствующих дуг (пусть пересечение AD и окружности — это X), PX и QX. При этом, в силу симметрии, углы BAD и BDA равны. Аналогично можно сказать и про CAD и CDA. А как тогда найти угловые величины нужных нам дуг?
Подсказка 3
Верно, угол BDA равен полуразности дуг AB и PX! Дуга AB нам известна, угол BDA тоже, значит можем вырезать PX, а значит, и QX. Осталось сделать это!
Пусть отрезок пересекает описанную окружность треугольника
в точке
Обозначим через
угол, опирающийся на дугу
не содержащую вершину
Пусть
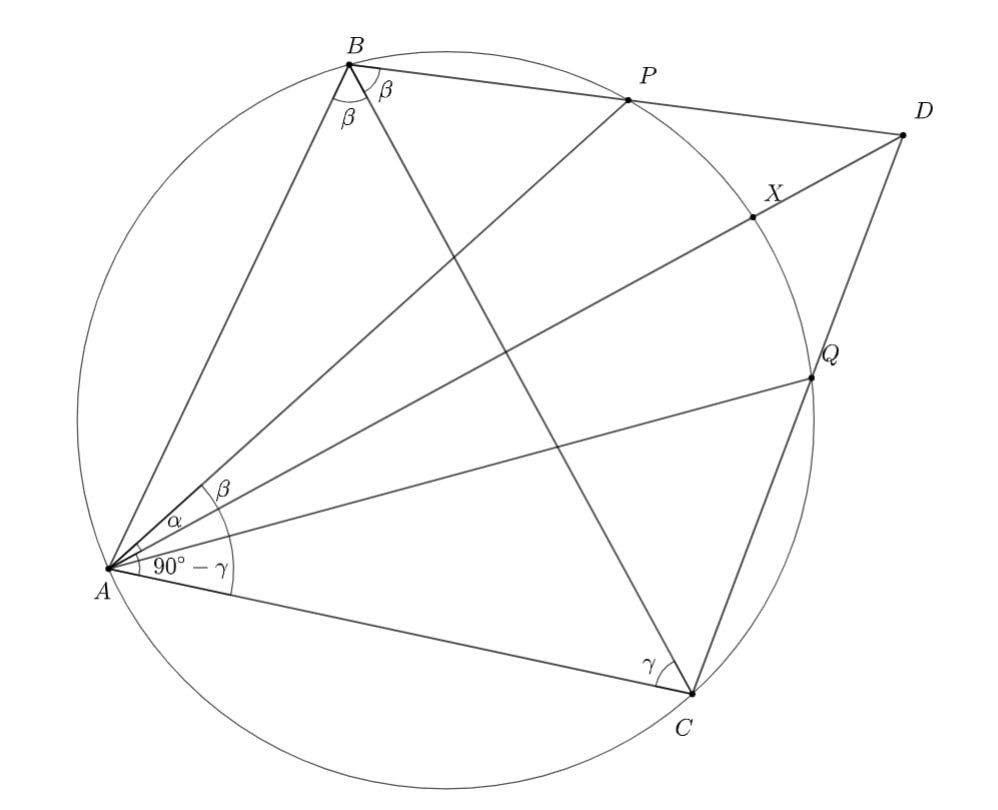
Тогда Из того, что точки
и
симметричны относительно
следует, что
Из
равенства вписанных углов
В итоге
Аналогично, угол, опирающийся на дугу не содержащую
также равен
(полученная нами запись
симметрична относительно
и
поэтому можно просто поменять
и
местами, далее рассуждения будут такими
же).
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




