Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
Четырёхугольник, диагонали которого взаимно перпендикулярны, вписан в окружность. Докажите, что основания перпендикуляров из точки пересечения его диагоналей на стороны образуют вписанный четырёхугольник.
Подсказка 1
В данном случае доказывать вписанность удобнее всего через сумму противоположных углов, потому что если провести диагонали, то получится слишком громоздкая картинка. Попробуйте ввести переменные (тут достаточно одной) и посчитать эти углы.
Подсказка 2
Удобно обозначить вписанный угол, опирающийся на какую-нибудь сторону исходного четырёхугольника, за α. Тогда можно поперебрасывать по вписанности этот угол и найти один из углов искомого четырёхугольника.
Подсказка 3
Так мы найдём угол 2α! Но тогда мы же знаем угол, опирающийся на противоположную хорду исходного четырёхугольника, чему он равен?
Подсказка 4
Из прямоугольного треугольника этот угол равен 90°-α, а значит, можно применить аналогичное рассуждение для противоположной стороны, и задача решится!
Первое решение. [ Окружность восьми точек.]
Обозначим основания перпендикуляров из точки пересечения диагоналей четырехугольника
через
а середины
сторон через
соответственно.
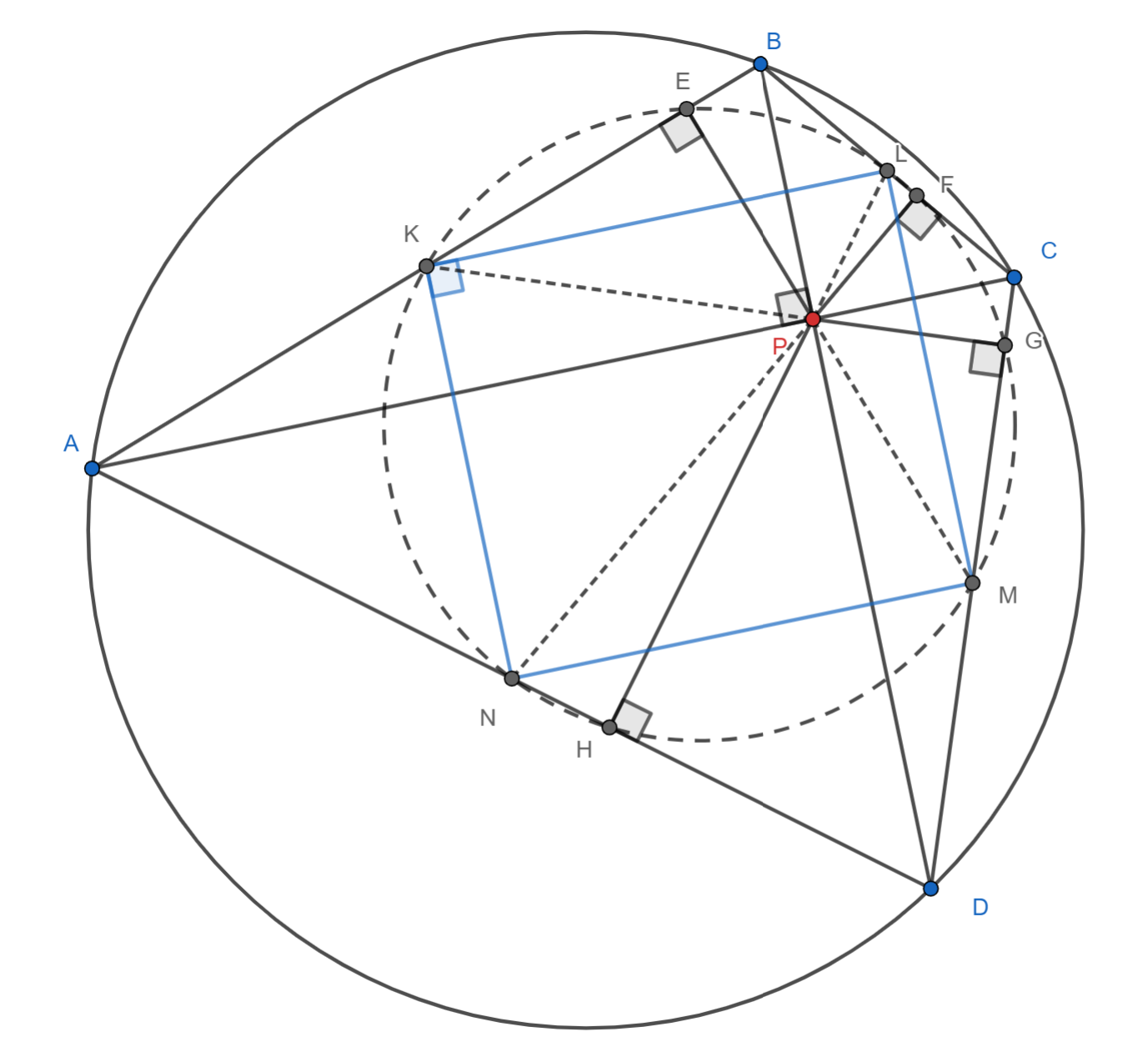
Для начала докажем, что (параллелограмм Вариньона для
) — прямоугольник.
Действительно, а
. Следовательно,
— вписанный.
Докажем, что прямая, содержащая отрезок перпендикулярна
[ Теорема Брахмагупты.]
Пусть эта прямая пересекает в точке
.
Действительно, как вертикальные,
как вписанные, опирающиеся на одну дугу. Следовательно,
по двум углам и
А значит,
лежит на окружности, описанной около
и является
основанием перпендикуляра, опущенного на
из точки
то есть точкой
.
Утверждение доказано.
Значит, точка лежит на окружности, описанной около
Аналогично доказывается, что и лежат на этой окружности, а значит,
— вписанный.
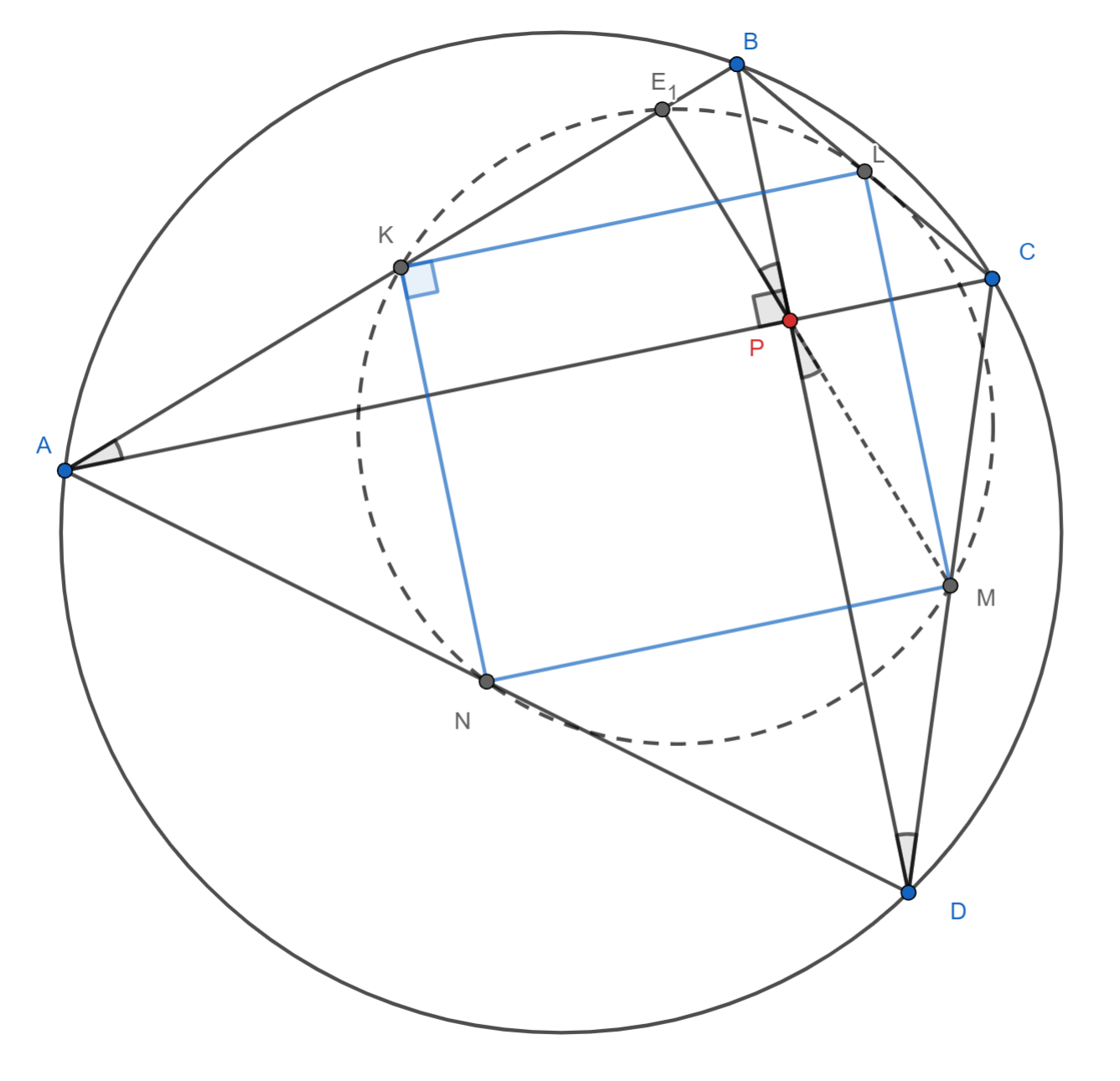
Второе решение.
.png)
Обозначим основания перпендикуляров из точки пересечения диагоналей четырехугольника
через
Посчитаем
углы:
Замечание.
Из второго решения легко заметить, что искомый по задаче четырёхугольник является не только вписанным, но и описанным. Центром вписанной в него окружности является точка пересечения диагоналей исходного четырёхугольника с перпендикулярными диагоналями.
Ответ убил.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




