Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
Внутри остроугольного треугольника нашлась такая точка
что
Лучи продлили до пересечения с описанной окружностью треугольника
Докажите, что полученные точки
пересечения лежат в вершинах равностороннего треугольника.
Подсказка 1
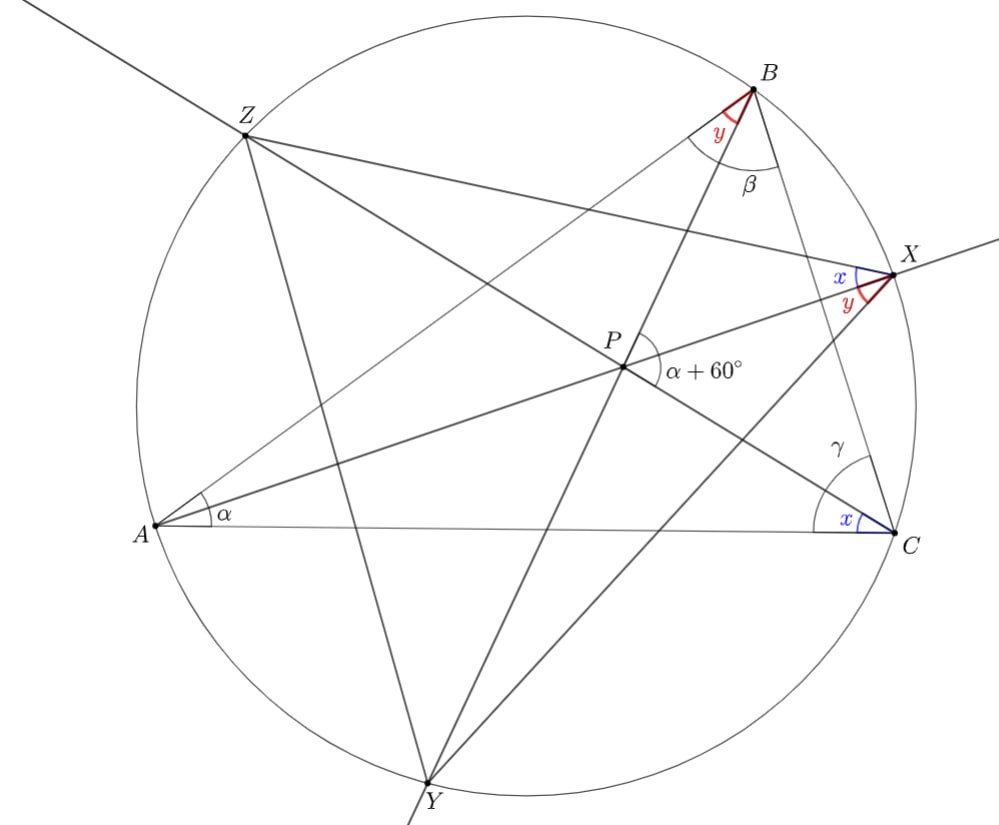
Сперва давайте обозначим всё полезное нам для решения: точки пересечения AP, BP, CP с окружностью за X, Y, Z, углы ∠PAC, ∠PCB, ∠PBA, ∠PCA, ∠PAB, ∠PBC. Время считать углы треугольника XYZ.
Подсказка 2
Посчитаем ∠ZXY (остальные аналогично). Из вписанности четырёхугольников AZXC и ABXY следует ∠ZXY=∠PCA+∠PBA . Осталось воспользоваться условиями о точке P.
Подсказка 3
Посчитаем угол ∠BPC как сумму ∠BPX+∠XPC, а они внешние в треугольниках APB и CBP. Записав условие ∠BPC=∠BAC+60°, выражаем ∠PCA+∠PBA.
Обозначим полученные точки пересечения лучей и
с описанной окружностью треугольника
соответственно как
и
а углы треугольника
как
Также проведем отрезки
и
и
как вписанные, опирающиеся на одну дугу.
Чтобы доказать, что треугольник — равносторонний, необходимо доказать, что его углы составляют Докажем, что
по свойству внешнего угла треугольника. В то же время
так как
Получаем
Аналогичным образом доказывается, что
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




