Вписанные углы и счёт углов в окружности
Ошибка.
Попробуйте повторить позже
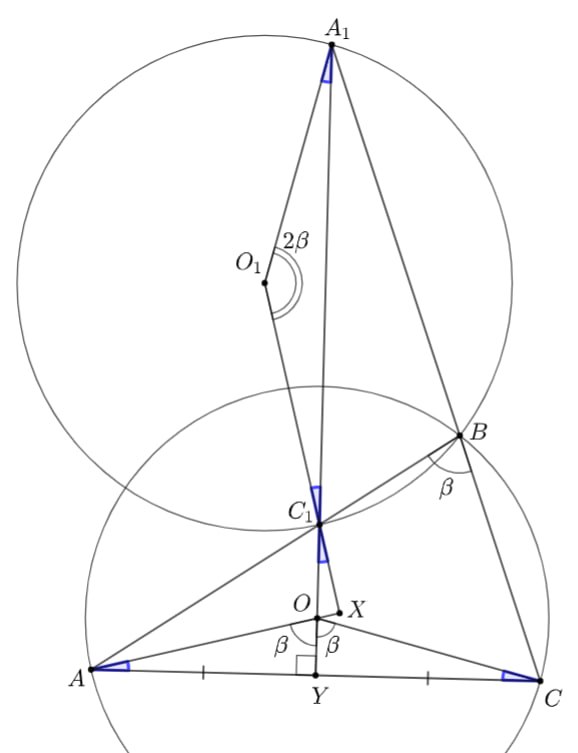
Серединный перпендикуляр к стороне треугольника
пересекает
и
в точках
и
соответственно. Точки
,
— центры описанных окружностей треугольников
и
соответственно. Докажите, что
Подсказка 1
Пересечём AO C₁O₁ в точке X, середину AC обозначим за Y. Требуется доказать, что ∠C₁XO₁=90°, при этом ∠C₁YA=90°. Давайте тогда сформулируем, что нам логично доказывать?
Подсказка 2
Ага, будем доказывать вписанность четырёхугольника C₁XYA. Это можно сделать, доказав равенство уголков ∠YAX и ∠YC₁X. Введём ∠ABC=β и выразим их.
Подсказка 3
Действительно, углы ∠AOC и ∠A₁O₁C₁ выражаются через ∠ABC как центральные углы треугольников ABC и A₁BC₁. Причём треугольники AOC и A₁O₁C₁ — равнобедренные, а, значит, зная выражение одного из углов через β, сможем посчитать и все остальные, в том числе искомые.
Пересечём и
в точке
Заметим, что достаточно доказать вписанность четырёхугольника
(
— середина
).
Обозначим угол
через
Угол
равен
как центральный. Треугольник
равнобедренный, значит
Угол равен
Следовательно,
как центральный. Треугольник
равнобедренный, значит
Мы получили равенство углов
и
что даёт нам нужную вписанность.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




